【题目】(本题满分12分)
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
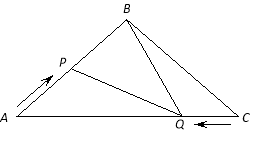
(1)、当x为何值时,PQ∥BC;
(2)、是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)、当![]() 时,求
时,求![]() 的值.
的值.
参考答案:
【答案】(1)、x=![]() ;(2)、AP=
;(2)、AP=![]() ;(3)、
;(3)、![]() .
.
【解析】
试题分析:(1)、根据PQ∥BC可得△APQ∽△ABC,从而求出x的值;(2)、根据相似三角形的性质可得![]() ,然后求出x的值;(3)、根据三角形的面积之比得出CQ:AC=1:3,根据AC的长度求出CQ的长度,然后计算出x的值,然后求出AP:AB的值,从而得出三角形的比值.
,然后求出x的值;(3)、根据三角形的面积之比得出CQ:AC=1:3,根据AC的长度求出CQ的长度,然后计算出x的值,然后求出AP:AB的值,从而得出三角形的比值.
试题解析:(1)、由题意知 AP=4x,CQ=3x若PQ∥BC 则△APQ∽△ABC
![]() ∵AB=BC=20 AC=30 ∴AQ=30―3x
∵AB=BC=20 AC=30 ∴AQ=30―3x
∴![]() ∴
∴![]() ∴当
∴当![]() 时,PQ∥BC.
时,PQ∥BC.
(2)、存在
∵△APQ∽△CQB 则![]() ∴
∴![]()
∴![]() ∴
∴![]() .
. ![]() .
.
∴当AP的长为![]() 时,△APQ∽△CQB
时,△APQ∽△CQB
(3)、∵![]() ∴
∴![]() 又∵AC=30 ∴CQ=10
又∵AC=30 ∴CQ=10
即![]()
![]() 此时,
此时,![]()
∴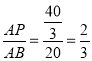 ∴
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中小学生每天锻炼一小时,句容某中学开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图(1)和图(2).
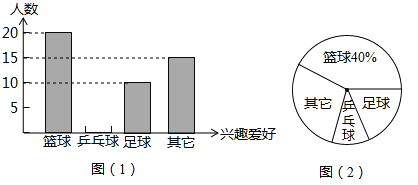
(1)某班同学的总人数为 人;
(2)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(3)扇形统计图(2)中表示”篮球”项目扇形的圆心角度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
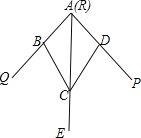
A.SAS B.ASA C.AAS D.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.

(1)求证:BD=CD.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳过运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)

A.abcd B.dabc C.dbca D.cabd
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A. 3,3,3 B. 5,5,11 C. 2,4,8 D. 1,2,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:a﹣(a﹣3b)= .
相关试题

