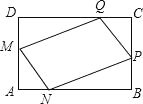
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围)
(2)当AN的长为多少米时种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元现设计要求种花的面积不大于440平方米,那么学校至少需要准备多少元费用.
参考答案:
【答案】(1)y1=40×24﹣y2=﹣2x2+64x,y2=2x2﹣64x+960;
(2)AN的长为10米或22米时种花的面积为440平方米;
(3)学校至少要准备140000元.
【解析】
试题分析:(1)根据三角形面积公式可得y2的解析式,再用长方形面积减去四个三角形面积,即可得y1的函数解析式;
(2)根据题意知y1=440,即即可得关于x的方程,解方程即可得;
(3)列出总费用的函数解析式,将其配方成顶点式,根据花的面积不大于440平方米可得x的范围,结合此范围根据二次函数性质即可得函数的最大值,从而得解.
试题解析:(1)根据题意,y2=2×![]() xx+2×
xx+2×![]() (40﹣x)(24﹣x)=2x2﹣64x+960,
(40﹣x)(24﹣x)=2x2﹣64x+960,
y1=40×24﹣y2=﹣2x2+64x;
(2)根据题意,知y1=440,即﹣2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(﹣2x2+64x)+100(2x2﹣64x+960)=﹣200(x﹣16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=﹣200(x﹣16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=10时,W取得最大值,最大值W=140000,
当x=22时,W取得最大值,最大值W=140000,
∴学校至少要准备140000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题:
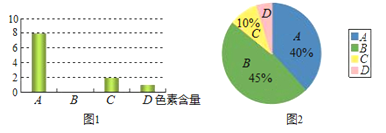
(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋? -
科目: 来源: 题型:
查看答案和解析>>【题目】“※”定义新运算:对于有理数a、b都有:a※b=ab-(a+b),那么5※3=__________;当m为有理数时,3※(m※2)=____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?
(3)在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中能够成立的是( )
A. (x+2y)2=x2+2xy+4y2 B. (x+2y)2=x2+4y2
C. (x﹣y)2=x2﹣2xy﹣y2 D. (a﹣b)2=(b﹣a)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式3x+2与代数式5x﹣10的值互为相反数,则x=_____
相关试题

