【题目】点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 坐标.
坐标.
(![]() )在
)在![]() 轴上方存在点
轴上方存在点![]() ,使以点
,使以点![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,画出
全等,画出![]() 并请直接写出点
并请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(![]() )
)![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(
;(![]() )作图见解析,点
)作图见解析,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】试题分析:
(1)如图1,分别以点B、C为圆心,BC为半径作圆交![]() 轴于点P1、P2、P3,作BC的垂直平分线交
轴于点P1、P2、P3,作BC的垂直平分线交![]() 轴于点P4,这4个点为所求点,结合已知条件求出它们的坐标即可;
轴于点P4,这4个点为所求点,结合已知条件求出它们的坐标即可;
(2)如图2,根据成轴对称的两个三角形全等,作出点C关于直线AB的对称点D,连接BD、AD,所得△ABD为所求三角形;再作出点D关于直线![]() 的对称点D1,连接AD1、BD1,所得△ABD1也是所求三角形;即有两个符合要求的三角形;
的对称点D1,连接AD1、BD1,所得△ABD1也是所求三角形;即有两个符合要求的三角形;
试题解析:
(![]() )如图1,∵点B、C的坐标分别为(0,2)、(1,0),
)如图1,∵点B、C的坐标分别为(0,2)、(1,0),
∴BC=![]() .
.
分别以点B、C为圆心,BC为半径作圆交![]() 轴于点P1、P2、P3,
轴于点P1、P2、P3,
则OP1=OB+BP1=OB+BC=![]() ,OP2=BP2-OB=BC-OB=
,OP2=BP2-OB=BC-OB=![]() ,OP3=OB=2;
,OP3=OB=2;
设OP4= ![]() ,则BP4=CP4=
,则BP4=CP4= ![]() ,在Rt△OCP4中,由勾股定理可得:
,在Rt△OCP4中,由勾股定理可得: ![]() ,解得:
,解得: ![]() ,即OP4=
,即OP4=![]() ;
;
∴①△P1BC是等腰三角形,BP1=BC,此时点P的坐标为![]() ;
;
②△P2BC是等腰三角形,BP2=BC,此时点P的坐标为![]() ;
;
③△P3BC是等腰三角形,P3C=BC,此时点P的坐标为![]() ;
;
④△P4BC是等腰三角形,BP4=CP4,此时点P的坐标为![]() .
.

(![]() )如图2,设点
)如图2,设点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() ≌
≌![]() ,
,
设过点![]() ,
, ![]() 的直线的解析式为
的直线的解析式为![]() .
.
则![]() ,
,
∴![]() ,
,
∴![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .
.
由![]() ,
,
解得![]() ,
,
∴![]() 点
点![]() .
.
∵![]() ,
,
∴![]() ,
,
根据对称性,点![]() 关于直线
关于直线![]() 的对称点D1
的对称点D1![]() 也满足条件.
也满足条件.
综上所述,满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足
 ,点C(m,n)在第一象限,已知
,点C(m,n)在第一象限,已知 是2的立方根.
是2的立方根.直接写出A,B,C三点的坐标;
求出△ABC的面积;
如图2,延长BC交y轴于D点,求点D的坐标;
如图3,过点C作CE∥AB交y轴于E点,求E点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司共有50名员工,为庆祝“五一”国际劳动节,公司将组织员工参加“海南双飞五日游”活动,旅行社的收费标准是每人2500元,公司提供下列两种方案供员工选择参与:
方案一:要参加旅游活动者,对于2500元的旅游费,员工个人支付500元,其余2000元由公司支付;
方案二:不参加旅游者,不必交费,每人还能领取公司发放的500元节日费.
(1)如果公司有30人参加旅游,其余20人不参加,问公司总共需支付多少元?
(2)如果公司共支付5.5万元,问有多少名员工参加旅游活动?
-
科目: 来源: 题型:
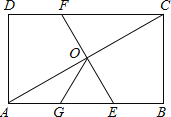
查看答案和解析>>【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG;(2)OG=
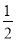 BC;(3)△OGE是等边三角形;(4)
BC;(3)△OGE是等边三角形;(4)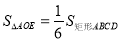 .
.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,
 .其中正确的是( )
.其中正确的是( )A. ②④ B. ②③ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级6个班举行毕业文艺汇演,每班3个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少6个.设舞蹈类节目有
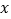 个.
个.(1)用含
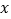 的代数式表示:歌唱类节目有______________个;
的代数式表示:歌唱类节目有______________个;(2)求九年级表演的歌唱类与舞蹈类节目数各有多少个?
(3)该校七、八年级有小品节目参与汇演,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计全场节目交接所用的时间总共16分钟.若从19:00开始,21:30之前演出结束,问参与的小品类节目最多能有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用普查方式的是( )
A.调查银川市市民垃圾分类的情况B.对市场上的冰淇淋质量的调查
C.对乘坐某次航班的乘客进行安全检查D.对全国中学生心理健康现状的调查
相关试题

