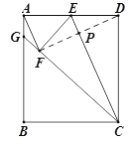
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.

参考答案:
【答案】(1)证明见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】(1)由对称的性质可得出相等的边与角,通过等腰三角形的性质及等量代换可得出∠EAF=∠DEC,即可证明AF∥CE;(2)连接DF,证△AFD、△EDC相似,根据相似的性质可推出线段AF,EF,EC之间的数量关系;(3)根据(2)中的数量关系: ![]() ,先求出EC、EF的长,进而可求出AF的长.
,先求出EC、EF的长,进而可求出AF的长.
(1)证明:由折叠矩形ABCD可得,EF=ED,CF=CD
∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°
∵点E为AD的中点
∴AE=ED=EF
∴∠EAF=∠EFA
∵∠DEF=∠EAF+∠EFA=∠DEC+∠FEC
∴∠EAF=∠DEC
∴AF∥EC
(2)线段AF,EF,EC之间的数量关系为: ![]() ,理由如下:
,理由如下:
连接DF交EC于P
∵EF=ED, CF=CD
∴E,C两点都在线段DF的中垂线上,即EC⊥DF
∴∠DPE=90°
∵AF∥EC
∴∠AFD=∠DPE=∠EDC=90°
∵∠EAF=∠DEC,∠AFD=∠EDC
∴△AFD∽△EDC
∴![]() ,即
,即![]()
∴![]()
(3)∵∠GAF+∠EAF=∠GFA+∠EFA=90°,∠EAF=∠EFA
∴∠GAF=∠GFA,∴AG=FG
在Rt△BGC中,∵BC=6,BG=8
∴![]()
∵AB=CD=CF,∴8+AG=10-FG,∴AG=FG=1,∴CF=CD=9
∵AD=BC=6,∴![]()
∴在Rt△DEC中, ![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则2019﹣a﹣b的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为2和4,则其周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若把代数式x2﹣4x﹣5化成(x﹣m)2+k的形式,其中m,k为常数,则m+k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的A,B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,若购买计算器的数量超过5个,分别用含x的式子表示出y1和y2;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,请问购买哪种品牌的计算器更合算?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形斜边上的中线等于斜边的________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )

A.(0,0)
B.( ,﹣
,﹣  )
)
C.(﹣ ,﹣
,﹣  )
)
D.(﹣ ,﹣
,﹣  )
)
相关试题

