【题目】如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
求证:(1)BD是⊙O的切线;(2)CE2=EH·EA.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出![]() ,即可得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,即可得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论.
,即可得出结论.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线。
(2)连接AC,
∵OF⊥BC,
∴![]() =
=![]() ,
,
∴∠ECB=∠CAE,
又∵∠HEC=∠CEA,
∴△CEH∽△AEC,
∴![]() =
=![]() ,
,
∴CE2=EH·EA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. 5a2-4a2=1B. 2a3+3a2=5a5C. 4a2b-3ba2=a2bD. 3a+2b=5ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,m2+1)一定在第__象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(a,b)和点B关于x轴对称,而点B与点C(2,3)关于y轴对称,那么a=__,b=__,点A和点C的位置关系是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,P在反比例函数y=
 (k<0)的图象上,点B,Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P,Q两点关于y轴对称,设点P的坐标为(m,n).
(k<0)的图象上,点B,Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P,Q两点关于y轴对称,设点P的坐标为(m,n).(1)求点A的坐标和k的值;
(2)求
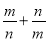 的值.
的值.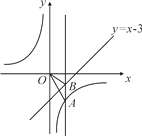
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(1,5),则另一个交点的坐标是( )
A.(1,﹣5)B.(5,﹣1)C.(﹣1,﹣5)D.(﹣5,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2012的坐标为______________.

相关试题

