【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为多少?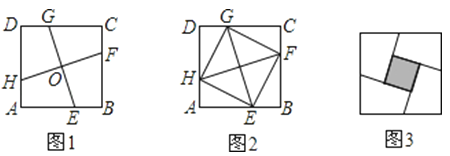
参考答案:
【答案】解:(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形.
(2)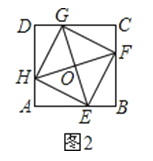
∵HA=EB=FC=GD=1,AB=BC=CD=AD=3,
∴GF=EF=EH=GH= ![]() =
=![]() ,
,
∵由(1)知,四边形EFGH是正方形,
∴GO=OF,∠GOF=90°,
由勾股定理得:GO=OF=![]() ,
,
∵S四边形FCGO=![]() ×1×2+
×1×2+![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴S阴影= (![]() +
+![]() )2﹣S四边形FCGO×4=10﹣9=1.
)2﹣S四边形FCGO×4=10﹣9=1.
【解析】(1)先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.
(2)根据已知条件,可以知道重新拼成的四边形是正方形(因为正方形GHEF的对角线翻到了外边,做了新拼成的正方形的边长),利用勾股定理求出GF和GO、FO的长,所的面积是10减去4个四边形GOFC的面积就是阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(3x+a)(x﹣2)的乘积中不含x一次项,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x为何值时,代数式x2-13x+12的值与代数式-4x2+18的值相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆是中心对称图形,它的对称中心是( )
A. 圆周 B. 圆心 C. 半径 D. 直径
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于中心对称的两个图形的关系是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
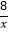 , 则有
, 则有
①它的图象在一、三象限:
②点(﹣2,4)在它的图象上;
③当l<x<2时,y的取值范围是﹣8<y<﹣4;
④若该函数的图象上有两个点A (x1 , y1),B(x2 , y2),那么当x1<x2时,y1<y2
以上叙述正确的是
相关试题

