【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 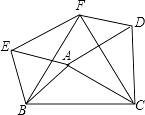
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足时,四边形AEFD是菱形.(无需证明) ②△ABC满足时,四边形AEFD是矩形.(无需证明)
③△ABC满足时,四边形AEFD是正方形.(无需证明)
参考答案:
【答案】
(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
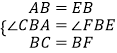 ,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
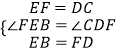 .
.
∴△EBF≌△DFC(SAS)
(2)证明:∵△EBF≌△DFC,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形
(3)AB=AC;∠BAC=150°;AB=AC,∠BAC=150°
【解析】(3)①若AB=AC,则平行四边形AEFD是菱形; 此时AE=AB=AC=AD,即△ABC是等腰三角形;
故△ABC满足AB=AC时,四边形AEFD是菱形;
②若∠BAC=150°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°﹣60°﹣60°﹣90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
③综合①②的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
故答案是:①AB=AC;
②∠BAC=150°;
③AB=AC,∠BAC=150°.
(1)由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;(2)利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;(3)①当AE=AD时,ADFE是菱形;②当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形;③当ADFE是正方形时,∠EAD=90°,且AE=AD,联立①②的结论即可.
【考点精析】通过灵活运用等边三角形的性质和平行四边形的判定与性质,掌握等边三角形的三个角都相等并且每个角都是60°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,B,C两点把线段AD分成4:5:7的三部分,E是线段AD的中点,CD=14厘米.
(1)求EC的长.
(2)求AB:BE的值.
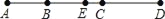
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD内两点M、N,满足MB⊥BC,MD⊥DC,NB⊥BA,ND⊥DA,若四边形BMDN的面积是菱形ABCD面积的
 ,则cosA= ______ .
,则cosA= ______ .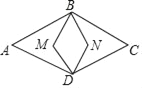
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活现象中,不是平移现象的是 ( )
A. 小亮荡秋千的运动B. 左右推动的推拉窗帘
C. 站在运行的电梯上的人D. 坐在直线行驶的列车上的乘客
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是它外角和的8倍,则这个多边形是______ 边形.
相关试题

