【题目】下列运算正确的是( )
A.m2+m2=2m2B.(m﹣n)(n﹣m)=n2﹣m2
C.(﹣2mn)2=﹣4m2n2D.(2m)3÷m3=2
参考答案:
【答案】A
【解析】
根据合并同类项、平方差公式、积的乘方、同底数幂的除法分别计算即可.
解:A.m2+m2=2m2,原计算正确,故此选项符合题意;
B.(m﹣n)(n﹣m)=﹣(n2﹣mn+m2),原计算错误,故此选项不符合题意;
C.(﹣2mn)2=4m2n2,原计算错误,故此选项不符合题意;
D.(2m)3÷m3=8m3÷m3=8,原计算错误,故此选项不符合题意.
故选:A.
-
科目: 来源: 题型:
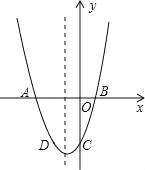
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中有4天空气质量为“优良”;③空气质量指数AQI与PM2.5浓度有关.其中正确的个数有( )

图(1)
图(2)
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
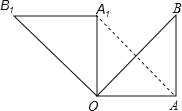
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生动地课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计,下面是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )

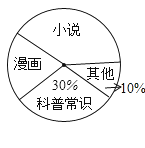
A.由这两个统计图可知喜欢“科学常识”的学生有90人
B.若该年级共有12000名学生,则由这两个统计图可估计喜爱“科学常识”的学生有360人
C.在扇形统计图汇总“漫画”所在扇形的圆心角为72°
D.由这两个统计图不能确定喜欢“小说”的人数 -
科目: 来源: 题型:
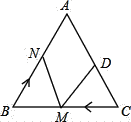
查看答案和解析>>【题目】如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是 厘米/秒.(直接写出答案)
-
科目: 来源: 题型:
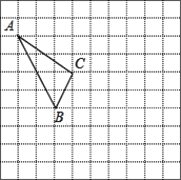
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
相关试题

