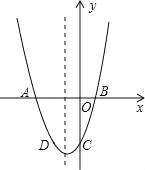
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
参考答案:
【答案】(1)一次函数解析式为y=x2+2x﹣3.(2)![]() (3)点P坐标为(0,﹣3)或(﹣2,﹣3)或(1+
(3)点P坐标为(0,﹣3)或(﹣2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).
【解析】
试题分析:(1)把A、D两点坐标代入二次函数y=x2+bx+c,解方程组即可解决.
(2)利用轴对称找到点P,用勾股定理即可解决.
(3)根据三角形面积公式,列出方程即可解决.
试题解析:(1)因为二次函数y=x2+bx+c的图象经过A(﹣3,0),D(﹣2,﹣3),所以![]() ,
,
解得![]() .
.
所以一次函数解析式为y=x2+2x﹣3.
(2)∵抛物线对称轴x=﹣1,D(﹣2,﹣3),C(0,﹣3),
∴C、D关于x轴对称,连接AC与对称轴的交点就是点P,
此时PA+PD=PA+PC=AC=![]() =
=![]() =
=![]() .
.
(3)设点P坐标(m,m2+2m﹣3),
令y=0,x2+2x﹣3=0,
x=﹣3或1,
∴点B坐标(1,0),
∴AB=4
∵S△PAB=6,
∴![]() 4
4![]() =6,
=6,
∴m2+2m﹣6=0,m2+2m=0,
∴m=0或﹣2或1+![]() 或1﹣
或1﹣![]() .
.
∴点P坐标为(0,﹣3)或(﹣2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】27的立方根为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2、4、5、6、8的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中有4天空气质量为“优良”;③空气质量指数AQI与PM2.5浓度有关.其中正确的个数有( )

图(1)
图(2)
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
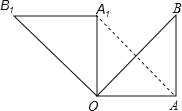
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.m2+m2=2m2B.(m﹣n)(n﹣m)=n2﹣m2
C.(﹣2mn)2=﹣4m2n2D.(2m)3÷m3=2
相关试题

