【题目】已知,如图,∠BAG=45°,∠AGD=135°,∠E=∠F.求证:∠BAE=∠CGF. 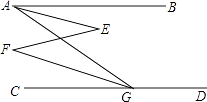
参考答案:
【答案】证明:∵∠BAG=45°,∠AGD=135°, ∴∠BAG+∠AGD=180°,
∴AB∥CD,
∴∠BAG=∠AGC,
∵∠E=∠F,
∴AE∥FG,
∴∠EAG=∠FGA,
∴∠BAG﹣∠EAG=∠CGA﹣∠FGA,
∴∠BAE=∠CGF
【解析】求出∠BAG+∠AGD=180°,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠BAG=∠AGC,根据平行线的判定得出AE∥FG,根据平行线的性质得出∠EAG=∠FGA,即可得出答案.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )

A.7(a+b+c﹣d) B.7(a+b﹣c+d)
C.7(a﹣b+c+d) D.7(b+c+d﹣a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点A、E、F、C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,且AB=CD,
(1)AB与CD平行吗?若平行请说明理由;
(2)证明BD平分EF.
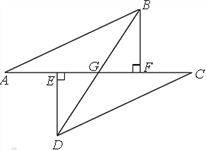
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC经过平移后,使点A与点A′(﹣1,4)重合.
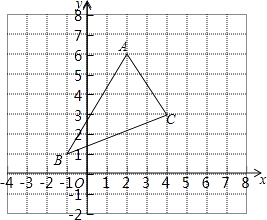
(1)画出平移后的△A′B′C′;
(2)求出△A′B′C′的面积;
(3)若三角形ABC内有一点P(a,b),经过平移后的对应点P′的坐标;
(4)若连接AA′,CC′,则这两条线段之间的关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣10)﹣(﹣2)+(﹣6)﹣11
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )

A.5个 B.4个 C.3个 D.2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,的两条直线叫做平行线.若直线与直线平行, 则记作 .
相关试题

