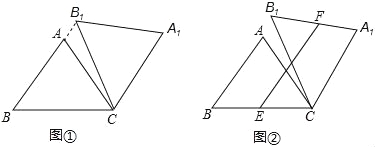
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
参考答案:
【答案】(1)①见试题解析;②![]() (3)
(3)![]() .
.
【解析】
试题分析:(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据三角函数和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
试题解析:(1)①证明:∵AB=AC,B1C=BC,∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),∴∠B1CA1=∠AB1C,∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①:
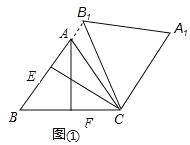
∵AB=AC,AF⊥BC,∴BF=CF,∵cos∠ABC=![]() ,AB=5,∴BF=3,∴BC=6,
,AB=5,∴BF=3,∴BC=6,
∴B1C=BC=6,∵CE⊥AB,∴BE=B1E=![]() ×6=
×6=![]() ,
,
∴BB1=![]() ,CE=
,CE=![]() ×6=
×6=![]() ,∴AB1=
,∴AB1=![]() -5=
-5=![]() ,
,
∴△AB1C的面积为:![]() ;
;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
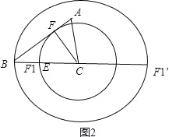
此时在Rt△BFC中,CF=![]() ,∴CF1=
,∴CF1=![]() ,
,
∴EF1的最小值为![]() -3=
-3=![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为9-![]() =
=![]() .
.
-
科目: 来源: 题型:
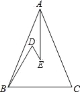
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,3)关于原点对称的点Q,则点Q的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A、B两镇相距x千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为u千米/小时、v千米/小时,并有:①出发后30分钟相遇;②甲到B镇后立即返回,追上乙时又经过了30分钟;③当甲追上乙时他俩离A镇还有4千米.求x、u、v.根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
A.x=u+4
B.x=v+4
C.2x-u=4
D.x-v=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】若2xa-1y2与-3x6y2b是同类项,则a、b的值分别为( )
A. a=7,b=1 B. a=7,b=3 C. a=3,b=1 D. a=1,b=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x-1向上平移3个单位长度,则平移后直线的解析式为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的长是3a,宽是2a-b,则长方形的周长是___________.
相关试题

