【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )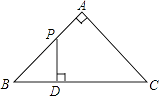
A.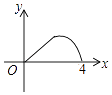
B.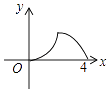
C.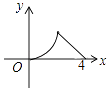
D.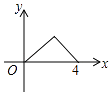
参考答案:
【答案】B
【解析】解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH= ![]() BC=2,
BC=2,
当0≤x≤2时,如图1,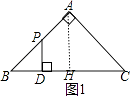
∵∠B=45°,
∴PD=BD=x,
∴y= ![]() xx=
xx= ![]() x2;
x2;
当2<x≤4时,如图2,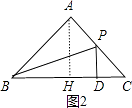
∵∠C=45°,
∴PD=CD=4﹣x,
∴y= ![]() (4﹣x)x=﹣
(4﹣x)x=﹣ ![]() x2+2x,
x2+2x,
故选B
过A点作AH⊥BC于H,利用等腰直角三角形的性质得到∠B=∠C=45°,BH=CH=AH= ![]() BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=
BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y= ![]() x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣
x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣ ![]() x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(1,0)、B(0,3)两点,对称轴是x=﹣1

(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OM上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,直接写出t的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC中,点D、E、F、分别为边AB,AC,BC的中点,M为直线BC动点,△DMN为等边三角形

(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立请说明理由;
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论是否仍然成立?若成立,请直接写出结论,若不成立请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.

(1)求线段AB所表示的y1与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣
 上,则使△ABC是直角三角形的点C的个数为( )
上,则使△ABC是直角三角形的点C的个数为( ) 
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣3|+
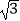 tan30°﹣
tan30°﹣  ﹣(2017﹣π)0 .
﹣(2017﹣π)0 .
相关试题

