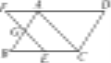
【题目】如图,在□ABCD中,点E在边BC上,点F在边DA的延长线上,且AF=CE,EF与AB交于点G.
(1)求证:AC∥EF;
(2)若点G是AB的中点,BE=6,求边AD的长.
参考答案:
【答案】(1)证明见解析(2)12
【解析】
(1)根据平行四边的判定与性质,可得答案;
(2)根据AAS证明△AGF≌△BGE,再根据全等三角形的性质与平行四边形的性质即可求解.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AF=CE,
∴四边形AFEC是平行四边形,
∴AC∥EF.
(2)∵AD∥BC,
∴∠F=∠GEB,
∵点G是AB的中点,
∴AG=BG.
在△AGF与△BGE中,
 ,
,
∴△AGF≌△BGE(AAS),
∴AF=BE=6.
∴AF=CE=6,
∴BC=BE+EC=12.
∵四边形ABCD是平行四边形,
∴AD=BC=12.
故答案为:(1)证明见解析(2)12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,
 表示5与 -2之差的绝对值,实际上也可以理解为 5 与 -2两数在数轴上所对的两点之间的距离,则使得
表示5与 -2之差的绝对值,实际上也可以理解为 5 与 -2两数在数轴上所对的两点之间的距离,则使得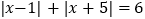 这样的整数
这样的整数 有____个.
有____个. -
科目: 来源: 题型:
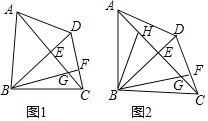
查看答案和解析>>【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知MN⊥PQ于点O,点A、
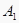 是以MN为轴的对称点,而点
是以MN为轴的对称点,而点 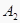 、A是以PQ为轴的对称点,求证:点
、A是以PQ为轴的对称点,求证:点 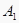 、
、 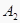 是以点O为对称中心的对称点.
是以点O为对称中心的对称点.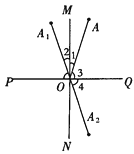
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是
 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型
价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?
-
科目: 来源: 题型:
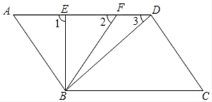
查看答案和解析>>【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
相关试题

