Question

【题目】如图1所示，已知函数y= (x＞0)图像上一点P，PA⊥x轴于点A（a，0），点B坐标为（0，b）(b>0) ．动点M是y轴正半轴上点B上方的点．动点N在射线AP上，过点B作AB的垂线，交射线AP于点D，交直线MN于点Q．连接AQ，取AQ的中点C．

(1)如图2，连接BP，求△PAB的面积；

(2)当点Q在线段BD上时, 若四边形BQNC是菱形，面积为2，求此时P点的坐标．

(3)在(2)的条件下，在平面直角坐标系中是否存在点S，使得以点D、Q、N、S为顶点的四边形为平行四边

形，如果存在，请直接写出所有的点S的坐标；如果不存在，请说明理由．

Answer 1

【答案】(1)、3；(2)、(3,2)；(3)、(1，4)，(1,0)，(5,4)

【解析】试题分析：(1)、连接OP，根据三角形的面积计算法则进行求解；(2)、根据四边形BQNC是菱形得出BQ=BC=NQ，∠BQC=∠NQC，根据AB⊥BQ，C是AQ的中点，得出BC=CQ=AQ，∠BQC=60°，∠BAQ=30°，从而说明△ABQ和△ANQ全等，得出∠BAQ=∠NAQ=30°，∠BAO=30°，设CQ=BQ=x，根据菱形的面积求出x的值，即BQ的长度，根据Rt△AQB的勾股定理求出OA的长度，根据反比例函数的性质得出点P的坐标.

试题解析：(1)、连接OP，S△PAB=S△PAO=xy=×6=3

(2)、∵四边形BQNC是菱形，∴BQ=BC=NQ，∠BQC=∠NQC

∵AB⊥BQ，C是AQ的中点，∴BC=CQ=AQ，∴∠BQC=60°，∠BAQ=30°

在△ABQ和△ANQ中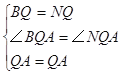∴△ABQ≌△ANQ ，∴∠BAQ=∠NAQ=30°，∴∠BAO=30°

∵S菱形BQNC==×CQ×BN，设CQ=BQ=x，则BN=2×（x×）=x，∴x=2，∴BQ=2

∵在Rt△AQB中，∠BAQ=30°，∴AB=BQ=2，∵∠BAO=30°∴OA=AB=3，

又∵P点在函数y=的图象上，∴P点坐标为（3，2）；

(3)、·