【题目】如图,在△ABC中,AB=BC , BD平分∠ABC . 过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E , BC交DE于点F , 连接CE . 求证:四边形BECD是矩形.
参考答案:
【答案】证明:∵AB=BC,BD平分∠ABC
∴AD=DC,BD⊥CA
∵AB∥DE, AD∥BE
∴四边形ABED是平行四边形
∴AD=BE,AD∥BE, AB=DE
∴DC=BE,DC∥BE
∴四边形BECD是平行四边形
∵BD⊥CA
∴∠BDC=90°![]()
∴四边形BECD是矩形
【解析】根据已知条件易推知四边形BECD是平行四边形. 结合等腰△ABC“三线合一”的性质证得BD⊥AC,即∠BDC=90°,由“有一内角为直角的平行四边形是矩形”得到◇BECD是矩形.
【考点精析】本题主要考查了角平分线的性质定理和等腰三角形的性质的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣2,y1),(﹣4,y,2)在函数y=x2﹣4x+7的图象上,那么y1 , y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD , 交DC的延长线于点E.求证:BC=DE
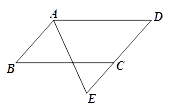
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )
A.①②③
B.①③④
C.②③
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
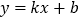 的图象经过点A(2,0),与y轴交于点B(0,4).
的图象经过点A(2,0),与y轴交于点B(0,4).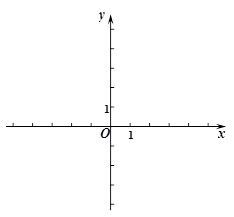
(1)求一次函数的表达式;并在平面直角坐标系内画出该函数的图象;
(2)当自变量x=-5时,求函数y的值;
(3)当x>0时,请结合图象,直接写出y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
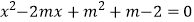 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)当m为正整数时,求方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是一个长为
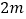 ,宽为
,宽为 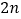 (
( 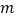 >
> 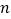 )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.
)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.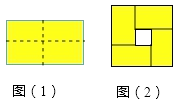
相关试题

