【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.

解:∵EF∥AD(已知)
∴∠2=∠3 )---①
又∵∠1=∠2(已知)
∴∠1=∠3( )----②
∴AB∥______( )----③
∴∠BAC+∠AGD=180°( )----④
∵∠BAC=70°(已知)
∴∠AGD=1800-700=1100
参考答案:
【答案】∠3;两直线平行,同位角相等;等量代换;DG,内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
【解析】试题分析:由EF与AD平行,利用两直线平行,同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与DG平行,利用两直线平行同旁内角互补得到两个角互补,即可求出所求角的度数.
解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG,内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(m,n)在第二象限,那么点B(﹣m,|n|)在( )
A.第一象限
B.第二象限;
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】2x2+3x+1=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-4,
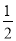 ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数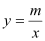 (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D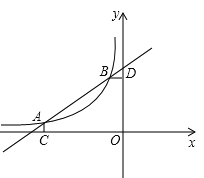
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
-
科目: 来源: 题型:
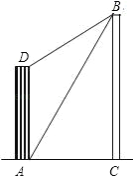
查看答案和解析>>【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂A、B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,有哪几种运输方案?请设计出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
相关试题

