【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.

(1)判断AG与⊙O的位置关系,并说明理由.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
参考答案:
【答案】(1)AG与⊙O相切,证明见解析;(2).
【解析】
试题分析:(1)直线与圆的位置关系有三种,相交,相切,相离,由图形显然AG与⊙O相切,再根据切线的判定定理,运用圆的性质和三角形的等边对等角证明AG垂直于半径OA即可.
(2)求线段OE的长,由题可知△OEF为直角三角形,所以考虑运用勾股定理求解.由圆的性质我们知道△ABC是直角三角形,根据相似三角形的性质可以求出线段EF、BF的长,从而在直角三角形OEF中勾股定理求解.
试题解析:(1)如图 连接OA,∵OA=OB,GA=GE,∴∠ABO=∠BAO,∠GEA=∠GAE.
∵EF⊥BC,∴∠BFE=90°.∴∠ABO+∠BEF=90°.又∵∠BEF=∠GEA,∴∠GAE=∠BEF.
∴∠BAO+∠GAE=90°. ∴OA⊥AG,即AG与⊙O相切.
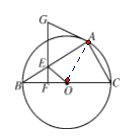
(2)解:∵BC为直径,∴∠BAC=90°.∵AC=6,AB=8,∴BC=10. ∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA.∴==.∴EF=1.8,BF=2.4,
∴OF=OB-BF=5-2.4=2.6. ∴OE==.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的运算正确的是( )
A. a+a2=a3 B. a2a3=a5 C. 6a﹣5a=1 D. a6÷a2=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a+a2=2a3
B.a2a3=a6
C.(2a4)4=16a8
D.(﹣a)6÷a3=a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在单项式3xy,x2y,y3中,请你写一个单项式,使一次单项式出现的频率为25% :_____。
-
科目: 来源: 题型:
查看答案和解析>>【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
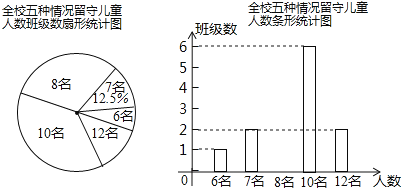
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
-
科目: 来源: 题型:
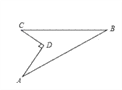
查看答案和解析>>【题目】如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
相关试题

