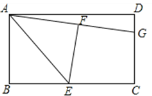
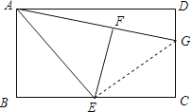
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
连接GE,根据点E是BC的中点以及翻折的性质可以求出BE=EF=EC,AF=AB,然后利用“HL”证明△GFE和△GCE全等,继而可得GF=GC=2,继而可得AG长,在Rt△ADG中,利用勾股定理求得AD的长即可求得答案.
连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,AF=AB,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=∠D=90°,BC=AD,AB=CD=CG+DG=2+1=3,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,
![]() ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC=2,
∴AG=AF+FG=3+2=5,
在Rt△ADG中,∠D=90°,
∴AD=![]() ,
,
∴BC=![]() ,
,
故选B.
-
科目: 来源: 题型:
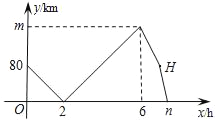
查看答案和解析>>【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:

(2)化简求值.2(
 -5y)-[-3(
-5y)-[-3( -3y)] ,其中
-3y)] ,其中 =
= ,y=-2
,y=-2(3)解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为____.
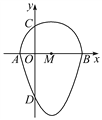
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )

A. 115°B. 125°C. 135°D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别在AB、AC上,BE与CD相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABE≌△ACD( )

A. AD=AEB. AB=AC
C. BE=CDD. ∠AEB=∠ADC
相关试题

