Question

【题目】如图，已知抛物线y=ax2-5ax+2（a≠0）与y轴交于点C，与x轴交于点A（1，0）和点B．

（1）求抛物线的解析式；

（2）求直线BC的解析式；

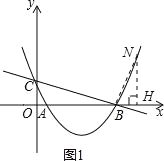
（3）若点N是抛物线上的动点，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似（排除全等的情况）？若能，请求出所有符合条件的点N的坐标；若不能，请说明理由．

Answer 1

【答案】（1）y=x2-x+2；（2）直线BC的解析式y=-x+2；（3）N点的坐标为（5，2）、（2，-1）或（-3，14）．

【解析】

试题分析：（1）把点A坐标代入抛物线y=ax2-5ax+2（a≠0）求得抛物线的解析式即可；

（2）求出抛物线的对称轴，再求得点B、C坐标，设直线BC的解析式为y=kx+b，再把B、C两点坐标代入线BC的解析式为y=kx+b，求得k和b即可；

（3）设N（x，ax2-5ax+2），分两种情况讨论：①△OBC∽△HNB，②△OBC∽△HBN，根据相似，得出比例式，再分别求得点N坐标即可．

试题解析：（1）∵点A（1，0）在抛物线y=ax2-5ax+2（a≠0）上，

∴a-5a+2=0，

∴a=，

∴抛物线的解析式为y=x2-x+2；

（2）抛物线的对称轴为直线x=，

∴点B（4，0），C（0，2），

设直线BC的解析式为y=kx+b，

∴把B、C两点坐标代入线BC的解析式为y=kx+b，得

，

解得k=-，b=2，

∴直线BC的解析式y=-x+2；

（3）设N（x，x2-x+2），分三种情况讨论：

①当△OBC∽△HNB时，如图1，

，

即，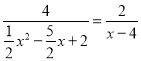

解得x1=5，x2=4（不合题意，舍去），

∴点N坐标（5，2）；

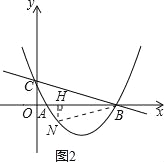
②当△OBC∽△HBN时，如图2，

，

即，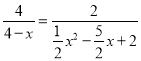

解得x1=2，x2=4（不合题意舍去），

∴点N坐标（2，-1）；

③当N（x，x2-x+2）在第二象限时，

H（x，0）在x轴的负半轴上，

∴BH=4-x，

∵△OBC∽△HNB，

∴，

即，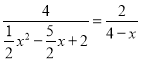

得到x2-x-12=0

解得x1=4（舍去）；x2=-3，

∴N点的坐标为（-3，14）

综上所述，N点的坐标为（5，2）、（2，-1）或（-3，14）,使得以点B、N、H为顶点的三角形与△OBC相似．