搜索
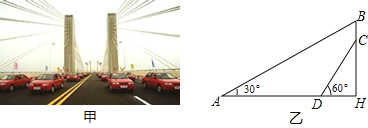
【题目】某大桥采用低塔斜拉桥桥型（如甲图），图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索CD与水平桥面的夹角是60°，两拉索顶端的距离BC为2米，两拉索底端距离AD为20米，请求出立柱BH的长．（结果精确到0.1米， 
≈1.73）
参考答案：
【答案】立柱BH的长约为16.3米．
【解析】试题分析：设DH=x米，由三角函数得出CH=
x，即可得BH=BC+CH=2+x，再求得AH=BH=2+3x，由AH=AD+DH得出方程2+3x=20+x，，解方程求出x，即可得出结果．
试题解析：设DH=x米，
∵∠CDH=60°，∠H=90°，
∴CH=DHsin60°=x，
∴BH=BC+CH=2+x，
∵∠A=30°，
∴AH=BH=2+3x，
∵AH=AD+DH，
∴2+3x=20+x，
解得：x=10﹣，
∴BH=2+（10﹣）=10﹣1≈16.3（米）．
答：立柱BH的长约为16.3米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】正比例函数y=（k+2）x，若y的值随x的值的增大而减小，则k的值可能是（ ）
A. 0B. 2C. -4D. -2
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题正确的是（ ）
A. 有一个角是直角的四边形是矩形
B. 对角线互相垂直的平行四边形是菱形
C. 对角线相等且互相垂直的四边形是正方形
D. 平行四边形的对角线相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=
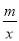（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，12），点C的坐标为（-4，0），且tan∠ACO=2．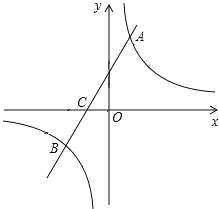
（1）求该反比例函数和一次函数的解析式；
（2）求点B的坐标；
（3）在x轴上求点E，使△ACE为直角三角形．（直接写出点E的坐标）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A（﹣1，0），B（5，﹣6），C（6，0）
（1）求抛物线的解析式；
（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC与点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止，在运动过程中，已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC与△DEF相似且周长比为2∶5，则△ABC与△DEF的面积比为 ．
相关试题
