【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
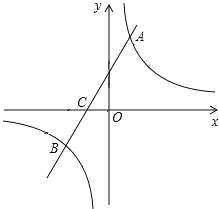
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
参考答案:
【答案】(1) y=![]() ,y=2x+8;(2) B(-6,-4);(3) 点E的坐标为E1(2,0),E2(26,0).
,y=2x+8;(2) B(-6,-4);(3) 点E的坐标为E1(2,0),E2(26,0).
【解析】
试题分析:(1)过点A作AD⊥x轴于D,根据A、C的坐标求出AD=12,CD=n+4,已知tan∠ACO=2,可求出n的值,把点的坐标代入解析式即可求得反比例函数和一次函数解析式;
(2)将反比例函数和一次函数的解析式联立,解方程组即可求得点B的坐标;
(3)分两种情况:①AE⊥x轴,②EA⊥AC,分别写出E的坐标即可.
试题解析:(1)过点A作AD⊥x轴于D,
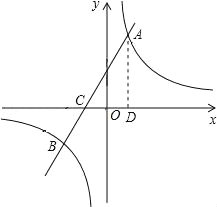
∵C的坐标为(-4,0),A的坐标为(n,12),
∴AD=12,CD=n+4,
∵tan∠ACO=2,
∴![]() =2,
=2,
解得:n=2,
∴A(2,12),
把A(2,12)代入y=![]() ,
,
得m=2×12=24,
∴反比例函数表达式为:y=![]() ,
,
又∵点A(2,12),C(-4,0)在直线y=kx+b上,
∴2k+b=12,-4k+b=0,
解得:k=2,b=8,
∴一次函数的表达式为:y=2x+8;
(2)由方程组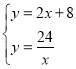 ,
,
解得: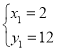 ,
,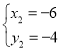 ,
,
∵A(2,12),
∴B(-6,-4);
(3)分两种情况:
①当AE⊥x轴时,即点E与点D重合,此时E1(2,0);
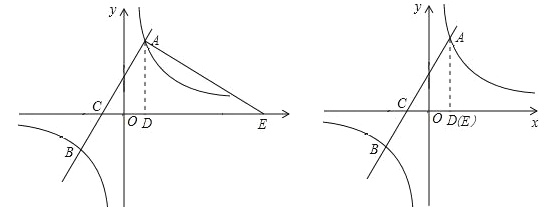
②当EA⊥AC时,此时△ADE∽△CDA,
则![]() ,
,
DE=![]() =24,
=24,
又∵D的坐标为(2,0),
∴E2(26,0).
综上所述,所求点E的坐标为E1(2,0),E2(26,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一粒米的质量约是0.000023kg,将数据0.000023用科学记数法表示为( )
A. 23×104 B. 2.3×104 C. 2.3×105 D. 2.3×10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=(k+2)x,若y的值随x的值的增大而减小,则k的值可能是( )
A. 0B. 2C. -4D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 有一个角是直角的四边形是矩形
B. 对角线互相垂直的平行四边形是菱形
C. 对角线相等且互相垂直的四边形是正方形
D. 平行四边形的对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
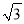 ≈1.73)
≈1.73)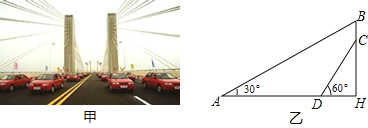
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.

(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
相关试题

