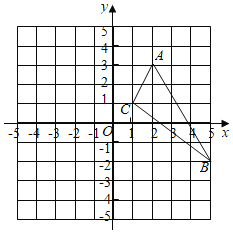
【题目】已知如图,在![]() 中,三个顶点的坐标分别为
中,三个顶点的坐标分别为![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,其 中点
,其 中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]()
![]() 直接写出平移后的
直接写出平移后的![]() 的顶点坐标:
的顶点坐标:
![]()
![]()
![]()
![]() 在坐标系中画出平移后的
在坐标系中画出平移后的![]()
![]() 求出
求出![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)详见解析;(3)5
;(2)详见解析;(3)5
【解析】
(1)已知![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,根据直角坐标系中坐标平移特点,A点横坐标减去4,纵坐标减2.即可得到D点坐标,同理得到E、F点坐标.
,根据直角坐标系中坐标平移特点,A点横坐标减去4,纵坐标减2.即可得到D点坐标,同理得到E、F点坐标.
(2)已知D(-2,1),E(1,-3),F(-3,-1),在直角坐标系中标注出D、E、F三点坐标,再连接DF,DE,EF,即可得到△DEF.
(3)由已知,![]() ,S△DEF=S矩形CGHE-S△DFG- S△DCE,即可求解.
,S△DEF=S矩形CGHE-S△DFG- S△DCE,即可求解.
(1)∵![]() ,将A沿
,将A沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度得到点D
个单位长度得到点D
∵2-4=-2,3-2=1
∴![]() 点坐标为(-2,1)
点坐标为(-2,1)
∵![]() ,将A沿
,将A沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度得到点E
个单位长度得到点E
∵5-4=1,-1-2=-3
∴![]() 点坐标为(1,-3)
点坐标为(1,-3)
∵![]() ,将A沿
,将A沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度得到点F
个单位长度得到点F
∵1-4=-3,1-2=-1
∴![]() 点坐标为(-3,-1)
点坐标为(-3,-1)
∴D(-2,1),E(1,-3),F(-3,-1)
故答案为:D(-2,1),E(1,-3),F(-3,-1)
(2)已知D(-2,1),E(1,-3),F(-3,-1),在直角坐标系中标注出D、E、F三点坐标,再连接DF,DE,EF,如图所示得到△DEF.
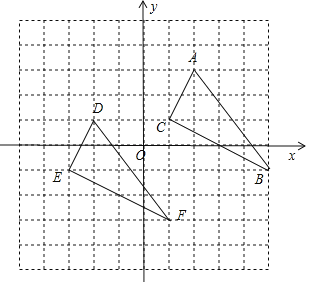
(3)∵![]()
∴S△DEF=S矩形CGHE-S△DFG-S△HFE-S△DCE![]()
故答案为:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后完成.
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为
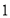 的
的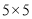 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
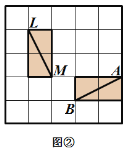
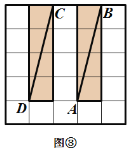
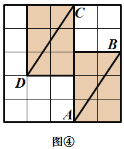
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知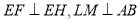 .在图③ 和图④中,可知
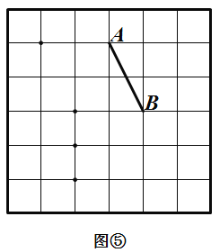
.在图③ 和图④中,可知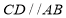 . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的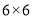 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段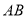 垂直 的线段(或者直线)
垂直 的线段(或者直线)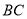 ,再画出与线段
,再画出与线段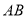 平行的一条线段(或者 直线)
平行的一条线段(或者 直线)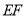 . 第二关:在图⑥的
. 第二关:在图⑥的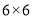 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)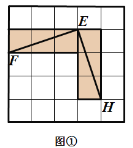

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=x+k和双曲线y=
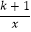 (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.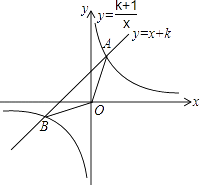
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1 , 当k=2时,△OAB的面积记为S2 , …,依此类推,当k=n时,△OAB的面积记为Sn , 若S1+S2+…+Sn=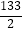 ,求n的值.
,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某项工程由甲、乙两队合做12天可以完成,共需工程费用27720元.乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, =
=  =
=  ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵ =
=  ∴b=
∴b=  =
=  =
=  =3
=3  .
.
理解应用:
如图,甲船以每小时30 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10  海里.
海里.
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

相关试题

