【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）（﹣2，1），先将△ABC沿一确定方向平移得到△A1B1C1 ， 点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 ， 点A1的对应点为点A2 ．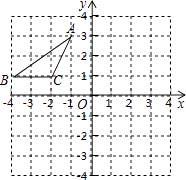

（1）画出△A1B1C1；
（2）画出△A2B2C2；
（3）求出在这两次变换过程中，点A经过点A1到达A2的路径总长．

参考答案：

【答案】
（1）解：如图，△A1B1C1为所作；


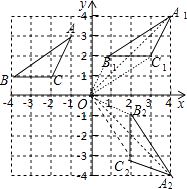
（2）解：如图，△A2B2C2为所作


（3）解：OA= =4 ，

点A经过点A1到达A2的路径总长= + = +2 π．


【解析】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．（1）由B点坐标和B1的坐标得到△ABC向右平移5个单位，再向上平移1个单位得到△A1B1C1 ， 则根据点平移的规律写出A1和C1的坐标，然后描点即可得到△A1B1C1；（2）利用网格特点和旋转的性质画出点A1的对应点为点A2 ， 点B1的对应点为点B2 ， 点C1的对应点为点C2 ， 从而得到△A2B2C2；（3）先利用勾股定理计算平移的距离，再计算以OA1为半径，圆心角为90°的弧长，然后把它们相加即可得到这两次变换过程中，点A经过点A1到达A2的路径总长．

关闭