搜索
【题目】先化简，再求值：（1+ 
）÷ 
，其中x=4﹣tan45°．
参考答案：
【答案】解：原式= 
= 
，
当x=4﹣tan45°=4﹣1=3时，原式= 
= 
．
【解析】先算括号里面的，再算除法，求出x的值代入进行计算即可．本题考查的是分式的化简求值，分式中的一些特殊求值题并非是一味的化简，代入，求值．许多问题还需运用到常见的数学思想，如化归思想（即转化）、整体思想等，了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助．
【考点精析】认真审题，首先需要了解特殊角的三角函数值(分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（ ）
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（ ）
①AE=BF；②AE⊥BF；③sin∠BQP=
；④S四边形ECFG=2S△BGE ． 
A.4
B.3
C.2
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC中，∠BAD=∠EBC，AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ；
(2)若∠ABC=35°，EG∥AD，EH⊥BE，求∠HEG的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C,得到△DCE.
（1）求证：△ACD≌△EDC;
（2）请探究△BDE的形状，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）（﹣2，1），先将△ABC沿一确定方向平移得到△A1B1C1 ， 点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 ， 点A1的对应点为点A2 ．
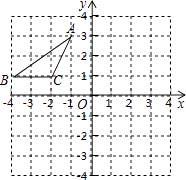
（1）画出△A1B1C1；
（2）画出△A2B2C2；
（3）求出在这两次变换过程中，点A经过点A1到达A2的路径总长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，∠AOB=90°，点C在射线OA上，CD∥OE．
（1）如图1，若∠OCD=120°，求∠BOE的度数；
（2）把“∠AOB=90°”改为“∠AOB=120°”，射线OE沿射线OB平移，得O′E，其他条件不变，（如图2所示），探究∠OCD、∠BO′E的数量关系；
（3）在（2）的条件下，作PO′⊥OB垂足为O′，与∠OCD的平分线CP交于点P，若∠BO′E=α，请用含α的式子表示∠CPO′（请直接写出答案）．
相关试题
