Question

【题目】【提出问题】

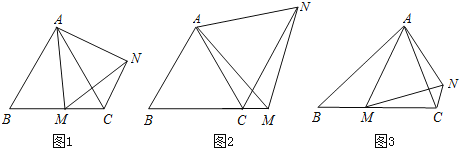
（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

【类比探究】

（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

【拓展延伸】

（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）结论∠ABC=∠ACN仍成立；理由见解析；（3）∠ABC=∠ACN．

【解析】

试题分析：（1）利用SAS可证明△BAM≌△CAN，继而得出结论；

（2）也可以通过证明△BAM≌△CAN，得出结论，和（1）的思路完全一样．

（3）首先得出∠BAC=∠MAN，从而判定△ABC∽△AMN，得到=，根据∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，得到∠BAM=∠CAN，从而判定△BAM∽△CAN，得出结论．

（1）证明：∵△ABC、△AMN是等边三角形，

∴AB=AC，AM=AN，∠BAC=∠MAN=60°，

∴∠BAM=∠CAN，

∵在△BAM和△CAN中，

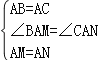
∴△BAM≌△CAN（SAS），

∴∠ABC=∠ACN．

（2）解：结论∠ABC=∠ACN仍成立；

理由如下：∵△ABC、△AMN是等边三角形，

∴AB=AC，AM=AN，∠BAC=∠MAN=60°，

∴∠BAM=∠CAN，

∵在△BAM和△CAN中，

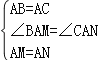
∴△BAM≌△CAN（SAS），

∴∠ABC=∠ACN．

（3）解：∠ABC=∠ACN；

理由如下：∵BA=BC，MA=MN，顶角∠ABC=∠AMN，

∴底角∠BAC=∠MAN，

∴△ABC∽△AMN，

∴=，

又∵∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，

∴∠BAM=∠CAN，

∴△BAM∽△CAN，

∴∠ABC=∠ACN．