【题目】二次函数 ![]() 的部分图像如图所示,图像过点
的部分图像如图所示,图像过点 ![]() ,对称轴为直线
,对称轴为直线 ![]() ,下列结论:(1)
,下列结论:(1) ![]() ;(2)
;(2) ![]() ;(3)若点
;(3)若点 ![]() 、点
、点 ![]() 、点
、点 ![]() 在该函数图像上,则
在该函数图像上,则 ![]() ;(4)若方程
;(4)若方程 ![]() 的两根为
的两根为 ![]() 和
和 ![]() ,且
,且 ![]() ,则
,则 ![]() .其中正确结论的序号是.
.其中正确结论的序号是.
参考答案:
【答案】(1)(4)
【解析】:∵抛物线的对称轴为直线x=- ![]() =2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=-
=2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=- ![]() =2,图象与x轴交于(-1,0),
=2,图象与x轴交于(-1,0),
∴抛物线x轴的另一个交点是(5,0),∵点A(-3,y1)、点B(- ![]() ,y2)、点C(
,y2)、点C( ![]() ,y3),∵
,y3),∵ ![]() -2=
-2= ![]() ,2-(-
,2-(- ![]() )=
)= ![]() ,∴
,∴ ![]() <
< ![]() ∴点C离对称轴的距离近,∴y3>y2,∵a<0,-3<-
∴点C离对称轴的距离近,∴y3>y2,∵a<0,-3<- ![]() <2,∴y1<y2∴y1<y2<y3,故(3)错误.如图,
<2,∴y1<y2∴y1<y2<y3,故(3)错误.如图,
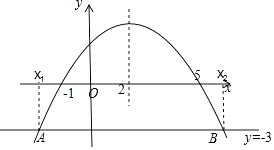
∵a<0,∴(x+1)(x-5)=-3/a>0,即(x+1)(x-5)>0,故x<-1或x>5,故(4)正确.
由抛物线的对称轴直线,得到4a+b=0,图象与x轴交于(-1,0),得到抛物线x轴的另一个交点,由已知得到点C离对称轴的距离近,得到y3>y2,由a<0,得到y1<y2<y3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段


(1)如图1,点
 沿线段
沿线段 自点
自点 向点
向点 以
以 的速度运动,同时点
的速度运动,同时点 沿线段点
沿线段点 向点
向点 以
以 的速度运动,几秒钟后,
的速度运动,几秒钟后, 两点相遇?
两点相遇?(2)如图1,几秒后,点
 两点相距
两点相距 ?
?(3)如图2,
 ,
, ,当点
,当点 在
在 的上方,且
的上方,且 时,点
时,点 绕着点
绕着点 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点 沿直线
沿直线 自
自 点向
点向 点运动,假若点
点运动,假若点 两点能相遇,求点
两点能相遇,求点 的运动速度.
的运动速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:
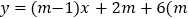 为常数,且
为常数,且 经过第四象限.
经过第四象限.
(1)若直线l与x轴交于点
 ,求m的值;
,求m的值;(2)求m的取值范围:
(3)判断点
 是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由.
是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
 求温馨提示牌和垃圾箱的单价各是多少元?
求温馨提示牌和垃圾箱的单价各是多少元? 如果该街道需购买温馨提示牌和垃圾箱共3000个.
如果该街道需购买温馨提示牌和垃圾箱共3000个. 求购买温馨提示牌和垃圾箱所需费用
求购买温馨提示牌和垃圾箱所需费用 元
元 与温馨提示牌的个数x的函数关系式;
与温馨提示牌的个数x的函数关系式; 若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的
若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的 倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 交x轴于A,交y轴于B,过B作
交x轴于A,交y轴于B,过B作 ,且
,且 ,点C在第四象限,点
,点C在第四象限,点 .
. 求点A,B,C的坐标;
求点A,B,C的坐标; 点M是直线AB上一动点,当
点M是直线AB上一动点,当 最小时,求点M的坐标;
最小时,求点M的坐标; 点P、Q分别在直线AB和BC上,
点P、Q分别在直线AB和BC上, 是以RQ为斜边的等腰直角三角形
是以RQ为斜边的等腰直角三角形 直接写出点P的坐标.
直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+
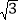 )
)B. 75°和(2,
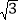 ﹣1)
﹣1)C. 15°和(2,1+
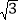 )或75°和(2,
)或75°和(2,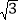 ﹣1)
﹣1)D. 15°和(2,1+
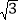 )或75°和(2,1﹣
)或75°和(2,1﹣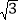 )
)
相关试题

