【题目】如图,矩形ABCD中,AB=8,AD=5,点E![]() 为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.

参考答案:
【答案】![]() 或
或![]()
【解析】分析:过点D′作MN⊥AB于点N,MN交CD于点M,由矩形有两条对称轴可知要分两种情况考虑,根据对称轴的性质以及折叠的特性可找出各边的关系,在直角△EMD′与△AND′中,利用勾股定理可得出关于DM长度的一元二次方程,解方程即可得出结论.
详解:过点D′作MN⊥AB于点N,MN交CD于点M,如图1、所示.
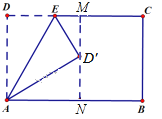
设DE=a,则D′E=a.
∵矩形ABCD有两条对称轴,
∴分两种情况考虑:
①当DM=CM时,
AN=DM=![]() CD=
CD=![]() AB=4,AD=AD′=5,
AB=4,AD=AD′=5,
由勾股定理可知:
ND′=![]() ,
,
∴MD′=MN-ND′=AD-ND′=2,EM=DM-DE=4-a,
∵ED′2=EM2+MD′2,即a2=(4-a)2+4,
解得:a=![]() ;
;
②当MD′=ND′时,
MD′=ND′=![]() MN=
MN=![]() AD=
AD=![]() ,
,
由勾股定理可知:
AN=![]() ,
,
∴EM=DM-DE=AN-DE=![]() -a,
-a,
∵ED′2=EM2+MD′2,即a2=(![]() a)2+(
a)2+(![]() )2,
)2,
解得:a=![]() .
.
综上知:DE=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() ..
..
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价x(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为
 ,
, ,猜想
,猜想 与
与 的关系式,并写出推导出过.
的关系式,并写出推导出过. -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨.梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=3m.
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度.(结果保留根号)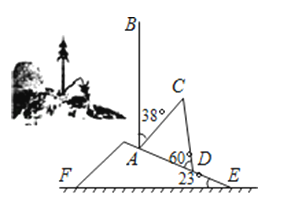
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:
x(元)
…
35
40
45
50
…
y(件)
…
750
700
650
600
…
若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
(1)求证:四边形CEDF是平行四边形;
(2)① 当AE= 时,四边形CEDF是矩形;
② 当AE= 时,四边形CEDF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
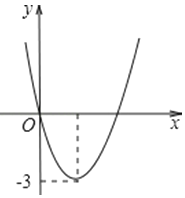
A.-3
B.3
C.-6
D.9
相关试题

