【题目】已知:如图,Rt△ABC中,∠ABC=90°,AD平分∠BAC交BC于D.
(1)用尺规作⊙O,使⊙O过A、D两点,且圆心O在AC上.(保留作图痕迹,不写作法)
(2)求证:BC与⊙O相切;
(3)设圆O交AB于点E,若AE=2,CD=2BD.求线段BE的长和弧DE的长.

参考答案:
【答案】(1)作图见解析; (2)证明见解析;(3)BE=1, ![]() 的长度为
的长度为![]() .
.
【解析】试题分析:(1)根据题意得:O点应该是AD垂直平分线与AC的交点;由此作AD的垂直平分线与AC交点即为圆心,然后以OA为半径即可作圆;
(2))由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AB∥OD,又由∠B=90°,则问题得证;
(3)连接OE,过点O作OF⊥AB于点F,
由垂径定理定理以及△AOF与△ACB相似推导得出AB的长,从而得BE的长,由OD∥AB可得△OCD∽△ACB,从而得出△AOE是等边三角形,进而推得∠EOD=60°,从而可得![]() 的长度.
的长度.
试题解析:(1)如图所示,⊙O即为所求:
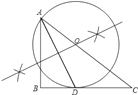
(2)连接OD,
∵OA=OD,∴∠OAD=∠ODA,
∵AD平分∠BAC,∴∠BAD=∠OAD,
∴∠BAD=∠ODA,∴OD∥AB,
∴∠ODC=∠ABC=90°,
∵OD是半径,
∴BC与⊙O相切;
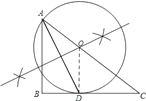
(3)连接OE,过点O作OF⊥AB于点F,
∵AE=2,∴由垂径定理定理可知:AF=1,
∵CD=2BD,∴ ![]() ,
, ![]() ,
,
∵OF∥BC,∴△AOF∽△ACB,
∴![]() ,
,
∵OF=BD,∴ ![]()
![]() ,
,
∴![]() ,∴AB=3,
,∴AB=3,
∴BE=AB-AE=1,
∵OD∥AB,∴△OCD∽△ACB,∴ ![]() ,
,
∴OD=2,∴OA=OD=AE,
∴△AOE是等边三角形,
∴∠AEO=60°,∵OD∥AB,∴∠EOD=60°,
∴![]() 的长度为
的长度为![]() =
= ![]() .
.
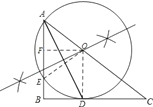
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明今年12岁,他爸爸今年36岁,几年后爸爸的年龄是小明年龄的2倍?(列方程并估计问题的解)
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x2﹣x+1=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】某人一天饮水1890毫升,将1890精确到1000后可以表示为( )
A. 0.189×104 B. 2×103 C. 1.89×103 D. 1.9×103
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx﹣4,当_____时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x﹣y=5且y﹣z=5,那么x﹣z的值是( )
A.5
B.10
C.﹣5
D.﹣10
相关试题

