【题目】定义:如图(1),若分别以△ABC的三边AC,BC,AB为边向三角形外侧作正方形ACDE,BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形. 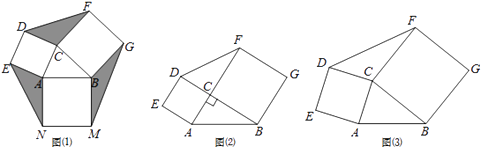
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2 . ①如图(2),当∠ACB=90°时,求证:S1=S2 .
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF,△AEN,△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.
参考答案:
【答案】
(1)证明:如图1,
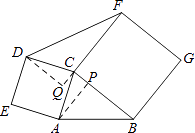
∵正方形ACDE和正方形BCFG,
∴AC=DC,BC=FC,∠ACD=∠BCF=90°,
∵∠ACB=90°,∴∠DCF=90°,
∴∠ACB=∠DCF=90°.
在△ABC和△DFC中,
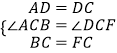 ,
,
∴△ABC≌△DFC(SAS).
∴S△ABC=S△DFC,
∴S1=S2
②S1=S2.理由如下:
解:如图3,过点A作AP⊥BC于点P,过点D作DQ⊥FC交FC的延长线于点Q.
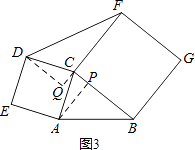
∴∠APC=∠DQC=90°.
∵四边形ACDE,BCFG均为正方形,
∴AC=CD,BC=CF,
∵∠ACP+∠ACQ=90°,∠DCQ+∠ACQ=90°.
∴∠ACP=∠DCQ.
在△APC和△DQC中
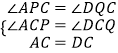 ,
,
∴△APC≌△DQC(AAS),
∴AP=DQ.
∴BC×AP=DQ×FC,
∴ ![]() BC×AP=
BC×AP= ![]() DQ×FC
DQ×FC
∵S1= ![]() BC×AP,S2=
BC×AP,S2= ![]() FC×DQ,
FC×DQ,
∴S1=S2
(2)由(2)得,S是△ABC面积的三倍,
要使S最大,只需三角形ABC的面积最大,
∴当△ABC是直角三角形,即∠ACB=90°时,S有最大值.
此时,S=3S△ABC=3× ![]() ×3×4=18
×3×4=18
【解析】(1)由正方形的性质可以得出AC=DC,BC=FC,∠ACB=∠DCF=90°,就可以得出△ABC≌△DFC而得出结论;(2)如图3,过点A作AP⊥BC于点P,过点D作DQ⊥FC交FC的延长线于点Q,通过证明△APC≌△DQC就有DQ=AP而得出结论;(3)如图 1,根据(2)可以得出S=3S△ABC , 要使S最大,就要使S△ABC最大,当∠AVB=90°时S△ABC最大,就可以求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个内角都是150°,这个多边形是 ( )
A. 八边形B. 十边形C. 十二边形D. 十四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n-
 ≤x<n+
≤x<n+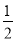 ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(
 x-1)=4,则实数x的取值范围是9≤x<11;
x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2 017x)=m+(2 017x);
⑤(x+y)=(x)+(y).
其中,正确的结论有________(填写所有正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市教育局对某镇实施“教育精准扶贫”,为某镇建中、小型两种图书室共30个.已知组建一个中型图书室需养殖类图书80本,种植类图书50本;组建一个小型图书室需养殖类图书30本,种植类图书60本.计划养殖类图书不超过2 000本,种植类图书不超过1 600本.
(1)符合题意的组建方案有几种?请写出具体的组建方案;
(2)若组建一个中型图书室的费用是2 000元,组建一个小型图书室的费用是1 500元,哪种方案费用最低?最低费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若5x=12,5y=4,则5x-y=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】52°25′12″=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
A. 矩形 B. 平行四边形 C. 正五边形 D. 正三角形
相关试题

