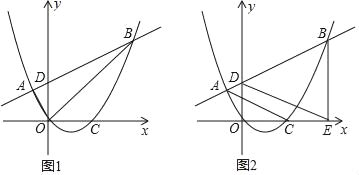
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.
参考答案:
【答案】(1)y=![]() x2﹣x;(2)2;(3) AC和DE的位置关系不变.
x2﹣x;(2)2;(3) AC和DE的位置关系不变.
【解析】分析:(1)由A、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设直线AD解析式为y=kx+m,把A点坐标代入可求得k与m的关系,联立直线AD与抛物线解析式,则可用m表示出B点横坐标,从而可用m表示出△AOB的面积,结合△AOB的面积为5可得到关于m的方程,可求得m的值;
(3)由A、C坐标可求得直线AC的解析式,用m可表示出D、E的坐标,则可表示出直线DE的解析式,则可证得结论.
详解:
(1)∵抛物线y=ax2+bx经过点A(﹣1,![]() )和点C(2,0),
)和点C(2,0),
∴ ,解得
,解得 ,
,
∴抛物线解析式为y=![]() x2﹣x;
x2﹣x;
(2)∵D(0,m),
∴可设直线AD解析式为y=kx+m,
把A点坐标代入可得![]() =﹣k+m,即k=m﹣
=﹣k+m,即k=m﹣![]() ,
,
∴直线AD解析式为y=(m﹣![]() )x+m,
)x+m,
联立直线AD与抛物线解析式可得 ,
,
消去y,整理可得![]() x2+(
x2+(![]() ﹣m)x﹣m=0,解得x=﹣1或x=2m,
﹣m)x﹣m=0,解得x=﹣1或x=2m,
∴B点横坐标为2m,
∵S△AOB=5,
∴![]() OD[2m﹣(﹣1)]=5,即
OD[2m﹣(﹣1)]=5,即![]() m(2m+1)=5,解得m=﹣
m(2m+1)=5,解得m=﹣![]() 或m=2,
或m=2,
∵点D(0,m)是y轴正半轴上一动点,
∴m=2;
(3)AC和DE的位置关系不变,证明如下:
设直线AC解析式为y=k′x+b′,
∵A(﹣1,![]() )、C(2,0),′
)、C(2,0),′
∴ ,解得
,解得 ,
,
∴直线AC解析式为y=﹣![]() x+1,
x+1,
由(2)可知E(2m,0),且D(0,m),
∴可设直线DE解析式为y=sx+m,
∴0=2ms+m,解得s=﹣![]() ,
,
∴直线DE解析式为y=﹣![]() x+m,
x+m,
∴AC∥DE,即AC和DE的位置关系不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE、DF.
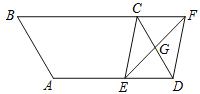
(1)求证:四边形CEDF是平行四边形;(2)当AE的长是多少时,四边形CEDF是矩形?
-
科目: 来源: 题型:
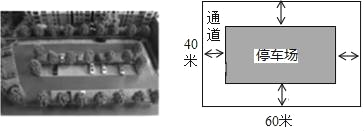
查看答案和解析>>【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法,其中正确的有( )
①如果a大于b,那么a的倒数小于b的倒数;②若a与b互为相反数,则
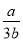 =﹣
=﹣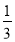 ;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,
;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,CE平分∠BCD,交直线AD于点E,若CD=6,AE=2,则tan∠ACE=______.
相关试题

