【题目】某水果批发商销售每箱进价为![]() 元的苹果,物价部门规定每箱售价不得高于
元的苹果,物价部门规定每箱售价不得高于![]() 元,市场调查发现,若每箱以
元,市场调查发现,若每箱以![]() 元的价格销售,平均每天销售
元的价格销售,平均每天销售![]() 箱,价格每提高
箱,价格每提高![]() 元,平均每天少销售
元,平均每天少销售![]() 箱.
箱.
求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
(元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
参考答案:
【答案】![]() ,当每箱苹果的销售价为
,当每箱苹果的销售价为![]() 元时,可以获得
元时,可以获得![]() 元的最大利润.
元的最大利润.
【解析】
根据平均每天销售量=90-超过50元的价格×3,则该批发商平均每天的销售利润w(元)=每箱的销售利润×每天的销售量,再根据题中所给的自变量的取值得到二次的最值问题即可.
由题意得:![]()
∴![]()
![]() ,
,
∵![]()
∴抛物线开口向下.
当![]() 时,
时,![]() 有最大值.
有最大值.
又∵![]() ,
,![]() 随
随![]() 的增大而增大.
的增大而增大.
∴当![]() 元时,
元时,![]() 的最大值为
的最大值为![]() 元.
元.
∴当每箱苹果的销售价为![]() 元时,可以获得
元时,可以获得![]() 元的最大利润.
元的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=5,BF=8则EF的长为__________.
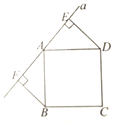
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
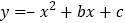 与
与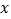 轴交于点
轴交于点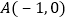 和点
和点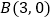 ,与
,与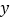 轴交于点
轴交于点 ,连接
,连接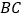 交抛物线的对称轴于点
交抛物线的对称轴于点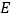 ,
, 是抛物线的顶点.
是抛物线的顶点.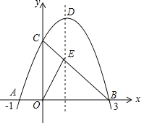
 求此抛物线的解析式;
求此抛物线的解析式; 直接写出点
直接写出点 和点
和点 的坐标;
的坐标; 若点
若点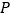 在第一象限内的抛物线上,且
在第一象限内的抛物线上,且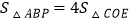 ,求
,求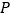 点坐标.
点坐标. -
科目: 来源: 题型:
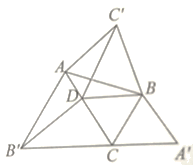
查看答案和解析>>【题目】如图所示,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC'、△BCA'、△CAB'都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
(1)证明:△C'BD≌△B'DC
(2)证明:△AC'D≌△DB'A
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示、方格纸中每个小正方的边长都是单位1,△ABC在平面直角坐标系中的位置图所示.
(1)将△ABC向右平移4个单位后得到△A
 B
B C
C ,请画出△A
,请画出△A B
B C
C ,并直接写出点C
,并直接写出点C 的坐标;
的坐标;(2)作出△A
 B
B C
C 关于x轴的对称图形△A
关于x轴的对称图形△A B
B C
C ,并直接写出点A
,并直接写出点A 的坐标;
的坐标;(3)请由图形直接判断以点C
 、C
、C 、B
、B 、B
、B ,为顶点的四边形是什么四边形?并求出它的面积.
,为顶点的四边形是什么四边形?并求出它的面积.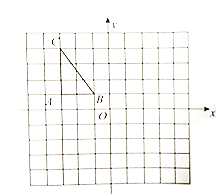
相关试题

