【题目】如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48) 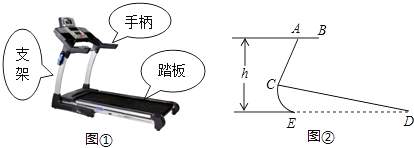
参考答案:
【答案】解:过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=∠FCD﹣∠ACD=∠CGD+∠CDE﹣∠ACD=90°+12°﹣80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=ACsin∠CAF≈0.744m,
在Rt△CDG中,CG=CDsin∠CDE≈0.42m,
∴h=0.42+0.74=1.156≈1.2(米),
答:手柄的一端A离地的高度h约为1.2m.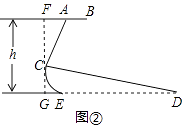
【解析】过C点作FG⊥AB于F,交DE于G.在Rt△ACF中,根据三角函数可求CF,在Rt△CDG中,根据三角函数可求CG,再根据FG=FC+CG即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:y=-
 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

-
科目: 来源: 题型:
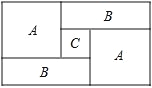
查看答案和解析>>【题目】如图,一个长方形运动场被分割成 A、B、A、B、C 共 5 个区域,A 区域是边长为 a 米的正方形,C 区是边长为 c 米的正方形
(1)列式表示一个 B 区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)当a=4,c=2时,求运动场地的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③
 ;④BD平分∠ADC;⑤∠BDC=
;④BD平分∠ADC;⑤∠BDC= ∠BAC.其中正确的结论有_______个.
∠BAC.其中正确的结论有_______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
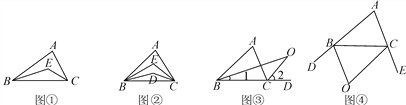
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

相关试题

