搜索
【题目】如图，已知点A1、A2、A3、…、An在x轴上，且OA1=A1A2=A2A3═An﹣1An=1，分别过点A1、A2、A3、…、An作x轴的垂线，交反比例函数y= 
（x＞0）的图象于点B1、B2、B3、…、Bn ， 过点B2作B2P1⊥A1B1于点P1 ， 过点B3作B3P2⊥A2B2于点P2 ， …，若记△B1P1B2的面积为S1 ， △B2P2B3的面积为S2 ， …，△BnPnBn+1的面积为Sn ， 则S1+S2+…+S2017= ． 
参考答案：
【答案】
【解析】解：根据题意可知：点B1（1，2）、B2（2，1）、B3（3， 
）、…、Bn（n， 
）， ∴B1P1=2﹣1=1，B2P2=1﹣ = 
，B3P3= ﹣ 
= 
，…，BnPn= ﹣ 
= 
，
∴Sn= AnAn+1BnPn= 
，
∴S1+S2+…+S2017= 
+ 
+ 
+…+ =1﹣ + ﹣ + ﹣ 
+…+ 
﹣ 
=1﹣ = ．
所以答案是： ．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，点P为射线BD，CE的交点．
（1）求证：BD=CE；
（2）若AB=2，AD=1，把△ADE绕点A旋转，
①当∠EAC=90°时，求PB的长；
②直接写出旋转过程中线段PB长的最小值与最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=
x2+bx﹣ 
的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．
（1）请直接写出点D的坐标：；
（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；
（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠BAC=45°，∠ACB=30°，将△ABC绕点A顺时针旋转得到△AB1C1 ， 当点C1、B1、C三点共线时，旋转角为α，连接BB1 ， 交AC于点D．下列结论：①△AC1C为等腰三角形；②△AB1D∽△BCD；③α=75°；④CA=CB1 ， 其中正确的是（ ）
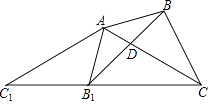
A.①③④
B.①②④
C.②③④
D.①②③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题
（1）计算：|
|+（ 
）﹣1﹣2cos45°
（2）解不等式组
，并把解集在数轴上表示出来． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正比例函数y=ax与反比例函数y=
（x＞0）的图象交于点M（ 
， ）．
（1）求这两个函数的表达式；
（2）如图1，若∠AMB=90°，且其两边分别于两坐标轴的正半轴交于点A、B．求四边形OAMB的面积．
（3）如图2，点P是反比例函数y= （x＞0）的图象上一点，过点P作x轴、y轴的垂线，垂足分别为E、F，PF交直线OM于点H，过作x轴的垂线，垂足为G．设点P的横坐标为m，当m＞ 时，是否存在点P，使得四边形PEGH为正方形？若存在，求出P点的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，已知CA=CB=5，BA=6，点E是线段AB上的动点（不与端点重合），点F是线段AC上的动点，连接CE、EF，若在点E、点F的运动过程中，始终保证∠CEF=∠B．
（1）求证：∠AEF=∠BCE；
（2）当以点C为圆心，以CF为半径的圆与AB相切时，求BE的长；
（3）探究：在点E、F的运动过程中，△CEF可能为等腰三角形吗？若能，求出BE的长；若不能，请说明理由．
相关试题
