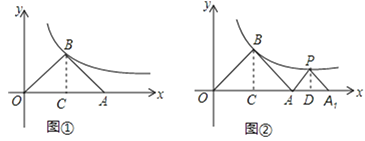
【题目】如图，在平面直角坐标系中，等腰三角形ABO的底边OA在x轴上，顶点B在反比例函数y= （x＞0）的图象上．当底边OA上的点A在x的正半轴上自左向右移动时，顶点B也随之在反比例函数y= （x＞0）的图象上滑动，但点O始终位于原点．

① ②

（1）如图①，若点A的坐标为（6，0）时，求点B的坐标；

（2）当点A移动到什么位置时，三角形ABO变成等腰直角三角形，请说明理由；

（3）在（2）中，如图②，△PA1A是等腰直角三角形，点P在反比例函数y= （x＞0）的图象上，斜边A1A都在x轴上，求点A1的坐标

参考答案：

【答案】（1）（3，4）（2）点A移动到（，0）时，△ABO变成等腰直角三角形（3）（，0）

【解析】试题分析：（1）过点B作BC⊥x轴于点C，由等腰三角形的三线合一，可得OC=AC=3，然后由顶点B在反比例函数y= （x＞0）的图象上，即可求得点B的坐标；（2）点A移动到（，0）时，△ABO变成等腰直角三角形，过点B作BC⊥x轴于点C，由等腰直角三角形的性质，可得OC=BC，设点B（a，a），然后由顶点B在反比例函数y= （x＞0）的图象上，求得点B的坐标，继而求得点A的坐标；（3）首先过点P作PD⊥x轴于点D，易得AD=PD，则可设AD=b，则点P（4+b，b），又由点P在反比例函数y= （x＞0）的图象上，求得b的值，继而求得答案．

试题解析：

（1）过点B作BC⊥OA于C，则OC=OA=3．

∴B的横坐标是3，把x=3代入y=

得：y=4．

则B的坐标是（3，4）．

（2）点A移动到（，0）时，△ABO变成等腰直角三角形．

理由：如图②，过点B作BC⊥x轴于点C，

∵△AOB是等腰直角三角形，

∴BC=OC= ,

设点B（a，a），

∵顶点B在反比例函数y= （x＞0）的图象上，

∴a= ，

解得：a=±（负值舍去），

∴OC=，

∴OA=2OC=，

∴点A移动到（，0）时，△ABO变成等腰直角三角形；

（3）如图②，过点P作PD⊥x轴于点D，

∵△PA1A是等腰直角三角形，

∴PD=AD，

设AD=b，则点P

∵点P在反比例函数

（x＞0）的图象上，

解得：(负的舍去)

∴

∴OA1=OA+AA1=

∴点A1的坐标是（，0）

关闭