Question

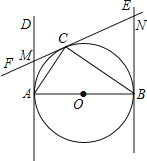
【题目】如图，已知AB为⊙O的直径，AB=2，AD和BE是圆O的两条切线，A、B为切点，过圆上一点C作⊙O的切线CF，分别交AD、BE于点M、N，连接AC、CB，若∠ABC=30°，则AM= ．

Answer 1

【答案】

【解析】

试题分析：连接OM，OC，由OB=OC，且∠ABC的度数求出∠BCO的度数，利用外角性质求出∠AOC度数，利用切线长定理得到MA=MC，利用HL得到三角形AOM与三角形COM全等，利用全等三角形对应角相等得到OM为角平分线，求出∠AOM为30°，在直角三角形AOM中，利用锐角三角函数定义即可求出AM的长．

解：连接OM，OC，

∵OB=OC，且∠ABC=30°，

∴∠BCO=∠ABC=30°，

∵∠AOC为△BOC的外角，

∴∠AOC=2∠ABC=60°，

∵MA，MC分别为圆O的切线，

∴MA=MC，且∠MAO=∠MCO=90°，

在Rt△AOM和Rt△COM中，

，

∴Rt△AOM≌Rt△COM（HL），

∴∠AOM=∠COM=∠AOC=30°，

在Rt△AOM中，OA=AB=1，∠AOM=30°，

∴tan30°=，即=，

解得：AM=．

故答案为：．