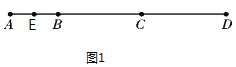
【题目】如图1,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 的路线以
的路线以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
![]()
(1)当![]() 时,则线段
时,则线段![]()
![]() ,线段
,线段![]()
![]() .
.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 的中点为
的中点为![]() ,问
,问![]() 的长是否变化?与点
的长是否变化?与点![]() 的位置是否无关?
的位置是否无关?
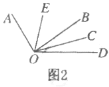
(4)知识迁移:如图2,已知![]() ,过角的内部任一点
,过角的内部任一点![]() 画射线
画射线![]() ,若
,若![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,问∠EOC的度数是否变化?与射线
,问∠EOC的度数是否变化?与射线![]() 的位置是否无关?
的位置是否无关?
参考答案:
【答案】(1)4,3;(2)![]() 或
或![]() ;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
【解析】
(1)根据线段的和差关系可得;(2)分情况讨论:)①当0≤t≤5时,此时点B从A向D移动;②当5<t≤10时,此时点B从D向A移动;(3)根据线段中点定义可得:EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=
AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)=![]() ∠AOD.
∠AOD.
解:(1)![]() 2×2=4(cm);
2×2=4(cm); ![]() =3(cm)
=3(cm)
![]()
(2)①当0≤t≤5时,此时点B从A向D移动:![]()
②当5<t≤10时,此时点B从D向A移动:![]()
(3)EC的长不变.与点B的位置无关.
∵AB中点为E,C是线段BD的中点,
∴EB=![]() AB,BC=
AB,BC=![]() BD.
BD.
∴EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD
AD
∵AD=10 cm,
∴EC=5cm,与点B的位置无关.
(4)∠EOC的度数不变,与射线OB的位置无关.

∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠EOC=∠EOB+∠BOC
=![]() (∠AOB+∠BOD)
(∠AOB+∠BOD)
=![]() ∠AOD
∠AOD
∵∠AOD=120°
∴∠EOC=60°,与OB位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学着说点理:补全证明过程:
如图,已知
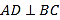 ,
,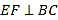 ,垂足分别为
,垂足分别为 ,
,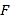 ,
,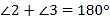 ,试证明:
,试证明: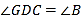 .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.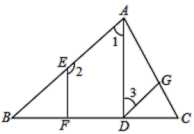
证明:∵
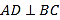 ,
,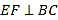 (已知)
(已知)∴
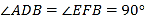 (___________________),
(___________________),∴
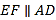 (___________________),
(___________________),∴________
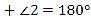 (___________________).
(___________________).又∵
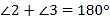 (已知),
(已知),∴
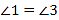 (___________________),
(___________________),∴
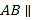 ________(___________________),
________(___________________),∴
 (___________________).
(___________________). -
科目: 来源: 题型:
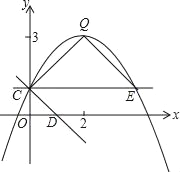
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(
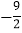 ,
, ),(
),(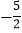 ,
,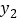 ),(
),( ,
,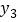 )是该抛物线上的点,则
)是该抛物线上的点,则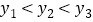 ,正确的个数有( )
,正确的个数有( )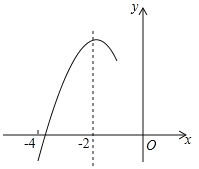
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )

A. 3 B.
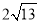 C.
C. 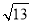 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细观察如图所示的折纸过程,然后回答下列问题:

(1)
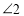 的度数为__________;
的度数为__________;(2)
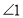 与
与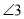 有何数量关系:______;
有何数量关系:______;(3)
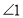 与
与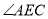 有何数量关系:__________;
有何数量关系:__________;
相关试题

