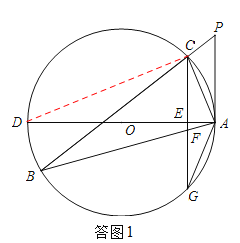
【题目】如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G。
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2![]() ,AB=4
,AB=4![]() ,求△AFG的面积.
,求△AFG的面积.

参考答案:
【答案】(1)PA与⊙O相切,理由见解析;(2)证明见解析;(3)3.
【解析】
试题分析:(1)连接CD,由AD为⊙O的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.
(2)连接BG,易证得△AFG∽△AGB,由相似三角形的对应边成比例,证得结论.
(3)连接BD,由AG2=AFAB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
试题解析:解:(1)PA与⊙O相切.理由如下:
如答图1,连接CD,
∵AD为⊙O的直径,∴∠ACD=90°.
∴∠D+∠CAD=90°.
∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.
∴∠PAC+∠CAD=90°,即DA⊥PA.
∵点A在圆上,
∴PA与⊙O相切.
(2)证明:如答图2,连接BG,
∵AD为⊙O的直径,CG⊥AD,∴![]() .∴∠AGF=∠ABG.
.∴∠AGF=∠ABG.
∵∠GAF=∠BAG,∴△AGF∽△ABG.
∴AG:AB=AF:AG. ∴AG2=AFAB.

(3)如答图3,连接BD,
∵AD是直径,∴∠ABD=90°.
∵AG2=AFAB,AG=AC=2![]() ,AB=4
,AB=4![]() ,∴AF=
,∴AF=![]() .
.
∵CG⊥AD,∴∠AEF=∠ABD=90°.
∵∠EAF=∠BAD,∴△AEF∽△ABD. ∴![]() ,即
,即![]() ,解得:AE=2.
,解得:AE=2.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈
 =
=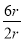 =3,那么当n=12时,π≈
=3,那么当n=12时,π≈ ≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
-
科目: 来源: 题型:
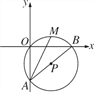
查看答案和解析>>【题目】如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
(1)求⊙P的半径及圆心P的坐标;
(2)M为劣弧OB的中点,求证:AM是∠OAB的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x2+x﹣1)x+3=1的所有整数解的个数是( )
A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】有甲乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲乙两个蓄水池中水的速度y(米)与注水时间x(小时)之间的函数图像如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= 的图象上,则k的值为( )
的图象上,则k的值为( )
A.-4 B.4 C.-2 D.2
相关试题

