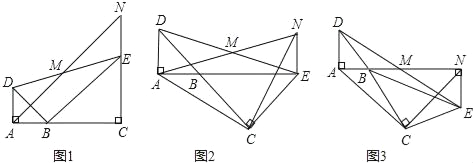
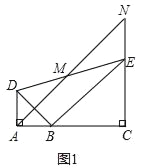
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 .
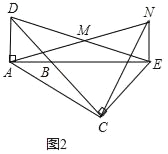
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.
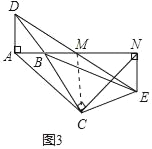
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3![]() ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 .
参考答案:
【答案】(1)AD=AE;(2)△ACN为等腰直角三角形,理由见解析;(3)![]() .
.
【解析】试题分析:(1)证明△ADM和△NEM全等,可得AD=NE.(2)△BAD和△BCE均为等腰直角三角形,证明△ABC和△NEC中,可得∠ABC=∠NEC,△ACN为等腰直角三角形.(3)连接CM,先证明△ADM≌△NEM,△ABC≌△NEC,所以 △ACN为等腰直角三角形,
由(1)可知,△AMD≌△NME,利用S四边形ACNE=S△AMC+S直角梯形MNEC.
试题解析:
解:(1)结论:AD=NE,
理由:如图1,
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM,
∵点M为DE的中点,
∴DM=EM,
在△ADM和△NEM中,
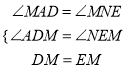 ,
,
∴△ADM≌△NEM,
∴AD=NE.
(2)结论:△ACN为等腰直角三角形.
理由,如图2,
∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°,
∵AD∥NE,
∴∠DAE+∠NEA=180°,
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=135°,
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°,
∴∠ABC=∠NEC,
∵△ADM≌△NEM(已证),
∴AD=NE,
∵AD=AB,
∴AB=NE,
在△ABC和△NEC中,
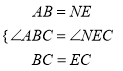 ,
,
∴△ABC≌△NEC,
∴AC=NC,∠ACB=∠NCE,
∴∠ACN=∠BCE=90°,
∴△ACN为等腰直角三角形.
(3)如图3中,连接CM.
∵AD∥NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE,
∵AD∥NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°,
∴∠FBC+∠FEC=360°﹣180°=180°
∵∠FBC+∠ABC=180°,
∴∠ABC=∠FEC,
在△ABC和△NEC中,
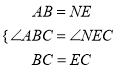 ,
,
∴△ABC≌△NEC,
∴AC=NC,∠ACB=∠NCE,
∴∠ACN=∠BCE=90°,
∴△ACN为等腰直角三角形,
由(1)可知,△AMD≌△NME,
∴AM=MN,AD=NE=1,
∴CM⊥AN,AM=CM=MN,
∵AC=3![]() ,
,
∴AM=CM=MN=3,
∴S四边形ACNE=S△AMC+S直角梯形MNEC=![]() ×3×3+
×3×3+![]() ×(3+1)×3=
×(3+1)×3=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:
 ≈1.73,结果保留整数)
≈1.73,结果保留整数)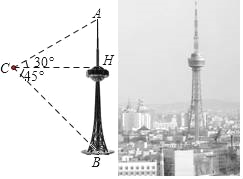
-
科目: 来源: 题型:
查看答案和解析>>【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个
81
85
90
93
95
98
100
人 数
1
2
8
11
5
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

-
科目: 来源: 题型:
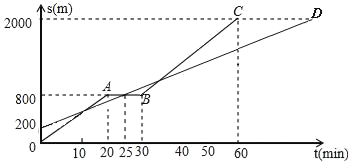
查看答案和解析>>【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少 分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y
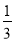 xb与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
xb与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
(1)求点A的坐标.
(2)在x轴上有一点P(m,0),过点P作x轴的垂线,与直线y
 xb交于点C,与直线y=x交于点D.若CD≥5,求m的取值范围.
xb交于点C,与直线y=x交于点D.若CD≥5,求m的取值范围. -
科目: 来源: 题型:
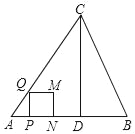
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠A=∠ADE,∠C=∠E.

(1)求证:BE∥CD;
(2)若∠EDC=3∠C,求∠C的度数.
相关试题

