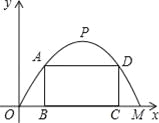
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
参考答案:
【答案】(1)M(12,0),P(6,6);(2)y=![]() x2+2x;(3)15米.
x2+2x;(3)15米.
【解析】试题分析:确定了抛物线的顶点式,可以设抛物线的顶点式,又过原点(0,0),就可以确定抛物线解析式;设OB=x,由对称性得CM=x,这样就可以用含x的式子表示AB、AD、CD了,为求三根木杆AB、AD、DC的长度之和的最大值,提供依据.
试题解析:(1)M(12,0),P(6,6)
(2)∵顶点坐标(6,6)
∴设y=a(x﹣6)2+6(a≠0)
又∵图象经过(0,0)
∴0=a(0﹣6)2+6
∴a=![]()
∴这条抛物线的函数解析式为y=![]() (x﹣6)2+6,即y=
(x﹣6)2+6,即y=![]() x2+2x;
x2+2x;
(3)设A(x,y)
∴A(x, ![]() (x﹣6)2+6)
(x﹣6)2+6)
∵四边形ABCD是矩形,
∴AB=DC=![]() (x﹣6)2+6,
(x﹣6)2+6,
根据抛物线的轴对称性,可得:OB=CM=x,
∴BC=12﹣2x,即AD=12﹣2x,
∴令L=AB+AD+DC=2[![]() (x﹣6)2+6]+12﹣2x=
(x﹣6)2+6]+12﹣2x=![]() x2+2x+12=
x2+2x+12=![]() (x﹣3)2+15.
(x﹣3)2+15.
∴当x=3,L最大值为15
∴AB、AD、DC的长度之和最大值为15米.
-
科目: 来源: 题型:
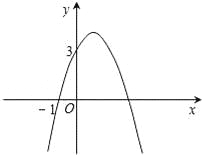
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三点A、B、C,请根据图回答下列问题:

(1)若将点B向左平移3个单位后,则A、B、C这三个点所表示的数谁最小?是多少?
(2)若将点A向右平移4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
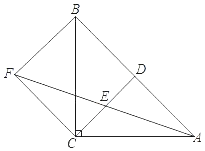
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:四边形BDCF是菱形;
(2)当Rt△ABC中的边或角满足什么条件时?四边形BDCF是正方形,请说明理由.
-
科目: 来源: 题型:
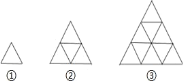
查看答案和解析>>【题目】下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
A. 63B. 60C. 56D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
相关试题

