【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 在抛物线上,直线
在抛物线上,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
①求证:![]() ;
;
②设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
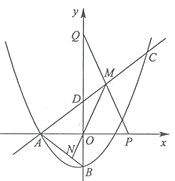
参考答案:
【答案】(1)c=-3; 直线AC的表达式为:y=![]() x+3;(2)①证明见解析;②
x+3;(2)①证明见解析;②![]()
【解析】
试题分析:(1)把点C(6,![]() )代入
)代入![]() 中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
(2)①分别求出tan∠OAB=tan∠OAD=![]() ,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明
,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明![]() ;
;
②过M点作ME⊥x轴,垂足为E,分别用含有m的代数式表示出AE和AM的长,然后利用![]() 即可求解.
即可求解.
试题分析:(1)把点C(6,![]() )代入
)代入![]()
解得:c=-3
∴![]()
当y=0时,![]()
解得:x1=-4,x2=3
∴A(-4,0)
设直线AC的表达式为:y=kx+b(k≠0)
把A(-4,0),C(6,![]() )代入得
)代入得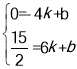
解得:k=![]() ,b=3
,b=3
∴直线AC的表达式为:y=![]() x+3
x+3
(2)①在RtΔAOB中,tan∠OAB=![]()
在RtΔAOD中,tan∠OAD=![]()
∴∠OAB=∠OAD
∵在RtΔPOQ中,M为PQ的中点
∴OM=MP
∴∠MOP=∠MPO
∵∠MPO=∠AON
∴∠APM=∠AON
∴ΔAPM∽ΔAON
②如图,过点M作ME⊥x轴于点E
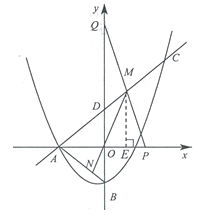
又∵OM=MP
∴OE=EP
∵点M横坐标为m
∴AE=m+4 AP=2m+4
∵tan∠OAD=![]()
∴cos∠EAM=cos∠OAD=![]()
∴AM=![]() AE=
AE=![]()
∵ΔAPM∽ΔAON
∴![]()
∴AN=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】大黄鱼是中国特有的地方性鱼类,有“国鱼”之称,由于过去滥捕等多种因素,大黄鱼资源已基本枯竭,目前,我市已培育出十余种大黄鱼品种,某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广,通过实验得知“甬岱”品种鱼苗成活率为
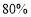 ,并把实验数据绘制成下列两幅统计图(部分信息未给出):
,并把实验数据绘制成下列两幅统计图(部分信息未给出):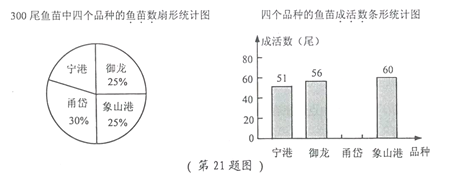
(1) 求实验中“宁港”品种鱼苗的数量;
(2) 求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形
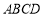 的四边
的四边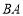 、
、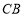 、
、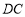 、
、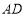 分别延长至
分别延长至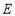 、
、 、
、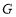 、
、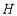 ,使得
,使得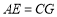 ,
,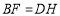 ,连接
,连接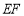 ,
,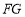 ,
,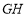 ,
,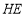 .
.(1) 求证:四边形
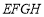 为平行四边形;
为平行四边形;(2) 若矩形
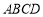 是边长为1的正方形,且
是边长为1的正方形,且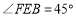 ,
,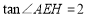 ,求
,求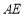 的长.
的长.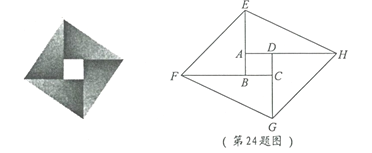
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是720°,这个多边形的边数是( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
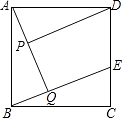
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=2x﹣1一定不经过第________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果-2amb2与3a5bn+1是同类项,那么m+n的值为______.
相关试题

