搜索
【题目】如图，己知△ABC，任取一点O，连接AO，BO，CO，并取它们的中点D，E，F，得△DEF，则下列说法：①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；③△ABC与△DEF的周长比为1∶2；④△ABC与△DEF的面积比为4∶1. 正确的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案：
【答案】D
【解析】
根据位似图形的性质，得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出②△ABC与△DEF是相似图形，再根据周长比等于位似比，以及根据面积比等于相似比的平方，即可得出答案．
根据位似性质得出：①△ABC与△DEF是位似图形，②△ABC与△DEF是相似图形．
∵将△ABC的三边缩小的原来的
，∴△ABC与△DEF的周长比为2：1，故③选项错误；根据面积比等于相似比的平方，∴④△ABC与△DEF的面积比为4：1．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一些相同的房间需要粉刷墙面．一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面．每名一级技工比二级技工一天多粉刷12m2墙面，求一个一级技工和一个二级技工每天粉刷的墙面各是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
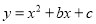经过点A（1,0）和B（0,3），其顶点为D.（1）求此抛物线的表达式；
（2）求△ABD的面积；
（3）设P为该抛物线上一点，且位于抛物线对称轴右侧，作PH⊥对称轴，垂足为H，若△DPH与△AOB相似，求点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，∠BCD=∠D=90°，E是边AB的中点.已知AD=1，AB=2.
（1）设BC=x，CD=y，求y关于x的函数关系式，并写出定义域；
（2）当∠B=70°时，求∠AEC的度数；
（3）当△ACE为直角三角形时，求边BC的长.
-
科目： 来源： 题型：
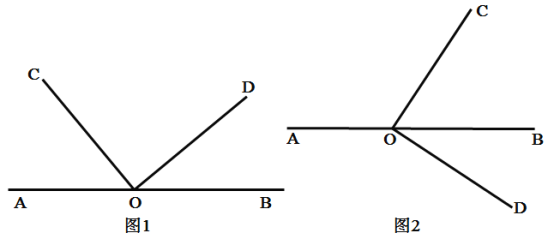
查看答案和解析>>【题目】如图，点O是直线AB上的一点，OD⊥OC，过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程)；
(2)当OD绕点O顺时针旋转一定的角度得到图2，使得直角边OC在直线AB的上方，若∠AOC=α，其他条件不变，依题意补全图形,并求∠DOE的度数（用含α的代数式表示）；
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有5张桌子时，两种摆放方式各能坐多少人？
（2）当有n张桌子时，两种摆放方式各能坐多少人？
（3）新学期有200人在学校就餐，但餐厅只有60张这样的餐桌，若你是老师，你打算选择哪种方式来摆放餐桌？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（2017浙江省湖州市）如图，已知∠AOB=30°，在射线OA上取点O1，以O1为圆心的圆与OB相切；在射线O1A上取点O2，以O2为圆心，O2O1为半径的圆与OB相切；在射线O2A上取点O3，以O3为圆心，O3O2为半径的圆与OB相切；…；在射线O9A上取点O10，以O10为圆心，O10O9为半径的圆与OB相切．若⊙O1的半径为1，则⊙O10的半径长是______．
相关试题
