【题目】景观大道要进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要370元;购买A种树苗5棵,B种树苗2棵,需要430元
(1)求购买A,B两种树苗每棵各需多少元?
(2)现需购买这两种树苗共100棵,要求购买这两种树苗的资金不超过5860元,求最多能购买多少棵A种树苗?
参考答案:
【答案】(1)购买A,B两种树苗每棵分别需70元,40元;(2)最多能购买62棵A种树苗.
【解析】
(1)设购进A种树苗的单价为x元/棵,购进B种树苗的单价为y元/棵,根据“购买A种树苗3棵,B种树苗4棵,需要370元;购买A种树苗5棵,B种树苗2棵,需要430元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设需购进A种树苗m棵,则购进B种树苗(100﹣m)棵,根据总价=单价×购买数量结合购买两种树苗的总费用不多于5860元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
解:(1)设购进A种树苗的单价为x元/棵,购进B种树苗的单价为y元/棵,则
![]()
解得![]() ,
,
答:购买A,B两种树苗每棵分别需70元,40元.
(2)设购进A种树苗m棵,则
70m+40(100﹣m)≤5860
解得 m≤62.
∴最多能购买62棵A种树苗.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某商店在2016年至2018年期间销售一种礼盒.2016年,该商店用2200元购进了这种礼盒并且全部售完:2018年,这种礼盒每盒的进价是2016年的一半,且该商店用2100元购进的礼盒数比2016年的礼盒数多100盒.那么,2016年这种礼盒每盒的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形的是( )
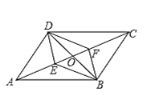
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式或不等式组
(1)3(x﹣1)<x﹣(2x﹣1)
(2)

(3)
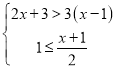
相关试题

