搜索
【题目】如图，正方形ABCD边长为4，点P从点A运动到点B，速度为1，点Q沿B﹣C﹣D运动，速度为2，点P、Q同时出发，则△BPQ的面积y与运动时间t（t≤4）的函数图象是（ ）
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：①点P在AB上运动，点Q在BC上运动，即0≤t≤2，
此时AP=t，BP=4﹣t，QB=2t，故可得y= 
PBQB= （4﹣t）2t=﹣t2+4t，函数图象为开口向下的抛物线；②点P在AB上运动，点Q在CD上运动，即2＜t≤4
此时AP=t，BP=4﹣t，△BPQ底边PB上的高保持不变，为正方形的边长4，
故可得y= BP×4=﹣2t+8，函数图象为直线．
综上可得全过程的函数图象，先是开口向下的抛物线，然后是直线；
故选：B．
本题应分两段进行解答，①点P在AB上运动，点Q在BC上运动，②点P在AB上运动，点Q在CD上运动，依次得出y与t的关系式即可得出函数图象．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．
（1）求经过A，B，C三点的抛物线的函数表达式；
（2）点P是线段BD上一点，当PE=PC时，求点P的坐标；
（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，AB=AC，D为BC的中点，以D为顶点作∠MDN=∠B．
（1）如图（1）当射线DN经过点A时，DM交AC边于点E，不添加辅助线，写出图中所有与△ADE相似的三角形．
（2）如图（2），将∠MDN绕点D沿逆时针方向旋转，DM，DN分别交线段AC，AB于E，F点（点E与点A不重合），不添加辅助线，写出图中所有的相似三角形，并证明你的结论．
（3）在图（2）中，若AB=AC=10，BC=12，当S△DEF=
S△ABC时，求线段EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O于点F，则∠BAF等于（ ）
A.12.5°
B.15°
C.20°
D.22.5° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一个等腰Rt△ABC对折，使∠A与∠B重合，展开后得折痕CD，再将∠A折叠，使C落在AB上的点F处，展开后，折痕AE交CD于点P，连接PF、EF，下列结论：①tan∠CAE=
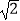﹣1；②图中共有4对全等三角形；③若将△PEF沿PF翻折，则点E一定落在AB上；④PC=EC；⑤S四边形DFEP=S△APF ． 正确的个数是（ ） 
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠CAB=30°，∠C=90°．AD=
AC，AB=8，E是AB上任意一点，F是AC上任意一点，则折线DEFB的最短长度为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线l：y=
x+1交x轴于点A，交y轴于点B，点A1、A2、A3 ， …在x轴的正半轴上，点B1、B2、B3 ， …在直线l上．若△OB1A1 ， △A1B2A2 ， △A2B3A3 ， …均为等边三角形，则△A6B7A7的周长是 ． 
相关试题
