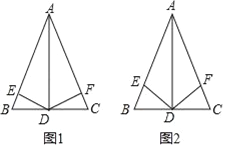
【题目】(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(2)如图2,在△ABC中,AB=AC,AD⊥BC,DE和DF分别平分∠ADB和∠ADC,求证:DE=DF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)在△ABC中,AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD,又因DE⊥AB,DF⊥AC,根据角平分线的性质定理即可证得DE=DF;(2)在△ABC中,AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD,∠ABD=∠CDA=90°,又因DE平分∠ADB,DF平分和∠ADC,可得∠ADE=∠ADF=45°,利用ASA证得△AED≌△AFD,根据全等三角形等的性质即可得结论.
试题解析:
(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC
∴DE=DF;
(2)证明:∵AB=AC,AD⊥BC
∴∠BAD=∠CAD,
∵DE平分∠ADB,DF平分和∠ADC,
∴∠ADE=∠ADF=45°,
在△AED和△AFD中,
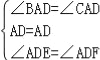 ,
,
∴△AED≌△AFD(ASA),
∴DE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
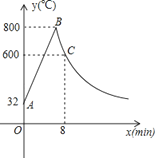
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进教育均衡发展,A市实行“阳光分班”,某校七年级一班共有新生45人,其中男生比女生多3人,求该班女生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A(a、b)是一次函数y=x+m的图像与反比例函数
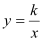 的图像在第一象限的交点,且S△ABO=3。
的图像在第一象限的交点,且S△ABO=3。
①根据这些条件你能够求出反比例函数的解析式吗?如果能够,请你求出来,如果不能,请说明理由。
②你能够求出一次函数的函数关系式吗?如果能,请你求出来,如果不能,请你说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;
 =1.44,
=1.44, =1.732,
=1.732, =2.236,以上数据供参考)
=2.236,以上数据供参考)
-
科目: 来源: 题型:
查看答案和解析>>【题目】既不是正数也不是负数的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个圆锥的高为
 cm,侧面展开图是半圆.
cm,侧面展开图是半圆.
求:(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积.
相关试题

