【题目】如图,Rt△ABO的顶点A(a、b)是一次函数y=x+m的图像与反比例函数![]() 的图像在第一象限的交点,且S△ABO=3。
的图像在第一象限的交点,且S△ABO=3。

①根据这些条件你能够求出反比例函数的解析式吗?如果能够,请你求出来,如果不能,请说明理由。
②你能够求出一次函数的函数关系式吗?如果能,请你求出来,如果不能,请你说明理由。
参考答案:
【答案】(1)![]() ,(2)不能,理由见解析。
,(2)不能,理由见解析。
【解析】本题考查的是函数的应用
(1)由△OAB的面积为3,可以求出反比例函数的系数为6,所以函数解析式为![]() ;
;
(2)根据这些条件不足以求出一次函数的关系式。由于点A的坐标并不确定,所以无法确定一次函数中的m,也就不能确定一次函数的关系式。实际上一次函数与反比例函数的交点以及坐标原点所构成的三角形的面积应该是一个定值,从这点也可以看出一次函数的解析式不是唯一的。
(1)设反比例函数的解析式为![]() ,
,
![]() 图象过点A(a、b),且
图象过点A(a、b),且![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() 点A(a、b)再第一象限,
点A(a、b)再第一象限,
![]() ,
,
![]() 反比例函数的解析式为
反比例函数的解析式为![]() ;
;
(2)由于点A的坐标并不确定,所以无法确定一次函数中的![]() ,也就不能确定一次函数的关系式。
,也就不能确定一次函数的关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的每个内角都是( )
A.60°
B.80°
C.100°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
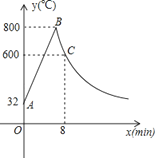
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进教育均衡发展,A市实行“阳光分班”,某校七年级一班共有新生45人,其中男生比女生多3人,求该班女生有多少人.
-
科目: 来源: 题型:
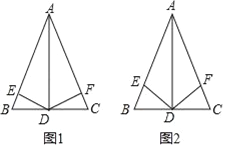
查看答案和解析>>【题目】(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(2)如图2,在△ABC中,AB=AC,AD⊥BC,DE和DF分别平分∠ADB和∠ADC,求证:DE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;
 =1.44,
=1.44, =1.732,
=1.732, =2.236,以上数据供参考)
=2.236,以上数据供参考)
-
科目: 来源: 题型:
查看答案和解析>>【题目】既不是正数也不是负数的数是 .
相关试题

