【题目】某校在七、八年级开展以“百日攻坚战,再上新台阶,建设新南平”为主题的征文活动,校学生会对这两个年级所有班级的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)投稿2篇的班级个数在扇形统计图中所对应的扇形的圆心角等于 °;
(2)求该校七、八年级各班投稿的平均篇数;
(3)投稿9篇的4个班级中,七、八年级各有两个班,学校准备从这四个中选出两个班代表学校参加上一级的比赛,请你用列表法或画树状图的方法求出所选两个班不在同一年级的概率.

参考答案:
【答案】(1)30;
(2)七、八年级各班投稿平均6篇;
(3)树状图见解析,P(所选两个班正好不在同一年级) ![]()
【解析】(1)根据投稿6篇的班级个数是3个,所占的比例是25%,可求总共班级个数,利用投稿篇数为2的比例乘以360°即可求解;
(2)根据加权平均数公式可求该校八,九年级各班在这一周内投稿的平均篇数,再用总共班级个数﹣不同投稿情况的班级个数即可求解:
(3)利用树状图法,然后利用概率的计算公式即可求解.
解:解:(1)3÷25%=12(个),
![]() ×360°=30°.
×360°=30°.
故投稿篇数为2所对应的扇形的圆心角的度数为30°;
(2)12﹣1﹣2﹣3﹣4=2(个),
(2+3×2+5×2+6×3+9×4)÷12
=72÷12
=6(篇),
所以该校七、八年级各班投稿平均6篇.
(3)设七年级两个班级为![]() ,八年级两个班级为
,八年级两个班级为![]() ,可列表如下:
,可列表如下:
|
|
|
| |
| ( | ( | ( | |
| ( | ( | ( | |
| ( | ( | ( | |
| ( | ( | ( |
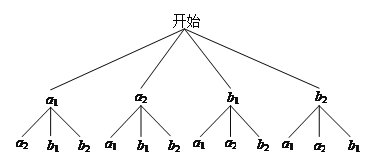
可画树状图如下:
一共12种情况,符合条件的有8种
∴P(所选两个班正好不在同一年级) ![]() .
.
“点睛”本题考查的是条形统计图、扇形统计图以及概率的计算的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式15m3n2+5m2n﹣20m2n的公因式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
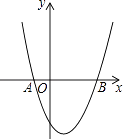
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:_____B:_____.
(2)观察数轴,与点A的距离为4的点表示的数是:_____.
(3)若将数轴折叠,使得A点与﹣2表示的点重合,则B点与数_____表示的点重合.
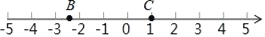
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a﹣2b)米的正方形,(0<b<
 ),
),
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形三边中有两边的长分别为4、9,则这个等腰三角形的周长为( )
A.13
B.17
C.22
D.17或22 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题5分)某服装店老板以60元的单价购进20件流行款的女服装,老板交代销售小姐以80元为标准价出售.针对不同的顾客,销售小姐对20件服装的售价不完全相同,她把超过80元的记为正数,其销售结果如下表所示:

该服装店在售完这20件服装后,请你通过计算说明该服装店老板是赚钱还是亏本?如果赚钱,那么赚了多少钱?如果亏本,那么亏了多少钱?
相关试题

