【题目】如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点. 
(1)判断A是否是PB的中点,并说明理由;
(2)若⊙O半径为8,试求BC的长.
参考答案:
【答案】
(1)解:A是PB的中点,
理由:连接AD,

∵CD是⊙O的直径,
∴AD⊥AC,
∵OB⊥AC,
∴AD∥OB,
∵PD=OD,
∴PA=AB,
∴A是PB的中点
(2)∵AD∥OB,
∴△APD∽△BPO,
∴ ![]() ,
,
∵⊙O半径为8,
∴OB=8,
∴AD=4,
∴AC= ![]() =4
=4 ![]() ,
,
∵OB⊥AC,
∴AE=CE=2 ![]() ,
,
∵OE= ![]() AD=2,
AD=2,
∴BE=6,
∴BC= ![]() =4
=4 ![]() .
.
【解析】(1)连接AD,由CD是⊙O的直径,得到AD⊥AC,推出AD∥OB,根据平行线等分线段定理得到PA=AB;(2)根据相似三角形的性质得到OB=8,求得AD=4,根据勾股定理得到AC= ![]() =4
=4 ![]() ,根据垂径定理得到AE=CE=2
,根据垂径定理得到AE=CE=2 ![]() ,由勾股定理即可得到结论
,由勾股定理即可得到结论
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生参观航天展览,甲、乙、丙、丁四位同学随机分成两组乘车.
(1)哪两位同学会被分到第一组,写出所有可能;
(2)用列表法(或树状图法)求甲、乙分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.

(1)如图①,当∠BAC=120°,∠DAE=60°时,求证DE=D'E.
(2)如图②,当DE=D'E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=
 (k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA= 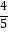 .
.
(1)求边AB的长;
(2)求反比例函数的解析式和m的值;
(3)若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一点
 从数轴上表示
从数轴上表示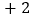 的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……(1)写出第一次移动后这个点在数轴上表示的数;
(2)写出第
 次移动后这个点在数轴上表示的数;
次移动后这个点在数轴上表示的数;(3)如果第
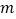 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求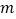 的值.
的值.
相关试题

