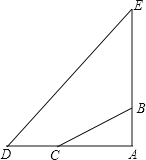
【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)
参考答案:
【答案】塔高AE为(80cos35°+30)tan50°m.
【解析】试题分析:根据锐角三角函数关系,得出cos∠ACB=![]() ,得出AC的长即可;利用锐角三角函数关系,得出tan∠ADE=
,得出AC的长即可;利用锐角三角函数关系,得出tan∠ADE=![]() ,求出AE即可.
,求出AE即可.
试题解析:在Rt△ABC中,∠ACB=35°,BC=80m,
∴cos∠ACB=![]() ,
,
∴AC=80cos35°,
在Rt△ADE中,tan∠ADE=![]() ,
,
∵AD=AC+DC=80cos35°+30,
∴AE=(80cos35°+30)tan50°.
答:塔高AE为(80cos35°+30)tan50°m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(3m+3n+2)(3m+3n-2)=77,那么m+n的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC与Rt△DEF的位置如图所示,其中AC=2
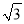 ,BC=6,DE=3
,BC=6,DE=3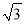 ,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.
,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.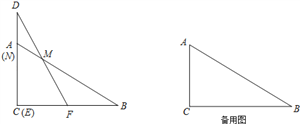
(1)当Rt△DEF在起始时,求∠AMF的度数;
(2)设BC的中点的为P,当△PBM为等腰三角形时,求t的值;
(3)若两个三角形重叠部分的面积为S,写出S与t的函数关系式和相应的自变量的取值范围.
-
科目: 来源: 题型:
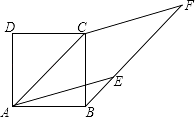
查看答案和解析>>【题目】如图,BF平行于正方形ABCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,则∠BCF的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P关于x轴的对称点P1的坐标是(2,1),那么点P关于原点的对称点P2的坐标是( )
A. (﹣1,﹣2) B. (2,﹣1) C. (﹣2,﹣1) D. (﹣2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
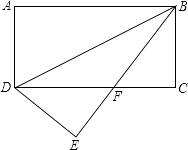
(1)求证:△EDF≌△CBF;
(2)求∠EBC. -
科目: 来源: 题型:
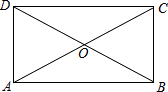
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为 .
相关试题

