【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=![]() (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
参考答案:
【答案】﹣9
【解析】
试题分析:作CE⊥OB于E,如图,根据反比例函数的比例系数k的几何意义得到S△OCE=S△BOD=![]() k,再根据三角形面积公式得到S△ACD=12,且OC=
k,再根据三角形面积公式得到S△ACD=12,且OC=![]() OA,则S△OAB=36+
OA,则S△OAB=36+![]() k,然后证明△OCE∽△OAQB,利用相似三角形的性质即可得到k的值.
k,然后证明△OCE∽△OAQB,利用相似三角形的性质即可得到k的值.
解:作CE⊥OB于E,如图,
∵点C、D在双曲线y=y=![]() (x<0)上,
(x<0)上,
∴S△OCE=S△BOD=![]() k,
k,
∵OC:AC=1:2,S△OCD=12,
∴S△ACD=24,OC=![]() OA,
OA,
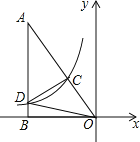
∴S△OAB=36+![]() |k|,
|k|,
∵CE∥AB,
∴△OCE∽△OAQB,
∴![]() =(
=(![]() )2,即
)2,即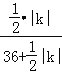 =
=![]() ,
,
∴k=±9.
∵k<0,
∴k=﹣9.
故答案为﹣9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(﹣2,y1),(﹣1,y2),(1,y3)在反比例函数y=
 的图象上,则下列说法正确的是( )
的图象上,则下列说法正确的是( )A.y1>y2>y3 B.y3>y2>y1 C.y3>y1>y2 D.y2>y1>y3
-
科目: 来源: 题型:
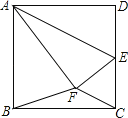
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知锐角△ABC中,AB、AC边的中垂线交于点O

(1)若∠A=α(0°<α<90°),求∠BOC;
(2)试判断∠ABO+∠ACB是否为定值;若是,求出定值,若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
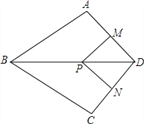
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值小于3的所有整数之和是( )
A. O B. 3 C. -3 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小华本学期都参加了5次数学考试(总分均为100分),数学老师想判断这两位同学的数学成绩谁更稳定,在作统计分析时,老师需比较这两人5次数学成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
相关试题

