【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.
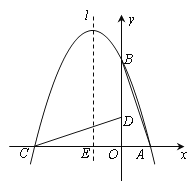
(1)求抛物线的解析式.
(2)若点P是第二象限内抛物线上的动点,其横坐标为t.
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标.
![]() ②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
参考答案:
【答案】(1) 抛物线的解析式为y=-x2-2x+3;(2) ①(-1,4)或(-2,3);②![]() .
.
【解析】
试题分析:(1)先求出A、B、C的坐标,再运用待定系数法就可以直接求出二次函数的解析式;
(2)①由(1)的解析式可以求出抛物线的对称轴,分类讨论当∠CEF=90°时,当∠CFE=90°时,根据相似三角形的性质就可以求出P点的坐标;
②先运用待定系数法求出直线CD的解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
试题解析:(1)在Rt△AOB中,OA=1,tan∠BAO=![]() =3,
=3,
∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=3,OD=OA=1,
∴A、B、C的坐标分别为(1,0),(0,3)(-3,0).
代入解析式为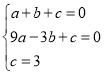 ,解得:
,解得: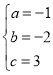 .
.
∴抛物线的解析式为y=-x2-2x+3;
(2)①∵抛物线的解析式为y=-x2-2x+3,
∴对称轴l=-![]() =-1,
=-1,
∴E点的坐标为(-1,0).
如图,当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(-1,4);
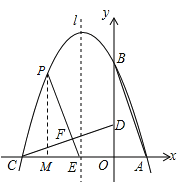
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.
∴![]() ,
,
∴MP=3EM.
∵P的横坐标为t,
∴P(t,-t2-2t+3).
∵P在第二象限,
∴PM=-t2-2t+3,EM=-1-t,
∴-t2-2t+3=-(t-1)(t+3),
解得:t1=-2,t2=-3(因为P与C重合,所以舍去),
∴t=-2时,y=-(-2)2-2×(-2)+3=3.
∴P(-2,3).
∴当△CEF与△COD相似时,P点的坐标为:(-1,4)或(-2,3);
②设直线CD的解析式为y=kx+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为:y=![]() x+1.
x+1.
设PM与CD的交点为N,则点N的坐标为(t,![]() t+1),
t+1),
∴NM=![]() t+1.
t+1.
∴PN=PM-NM=-t2-2t+3-(![]() t+1)=-t2-
t+1)=-t2-![]() t+2.
t+2.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=![]() PN
PN![]() CM+
CM+![]() PN
PN![]() OM
OM
=![]() PN(CM+OM)
PN(CM+OM)
=![]() PN
PN![]() OC
OC
=![]() ×3(-t2-
×3(-t2-![]() t+2)
t+2)
=-![]() (t+
(t+![]() )2+
)2+![]() ,
,
∴当t=-![]() 时,S△PCD的最大值为
时,S△PCD的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是( )

A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线
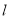 过点A(—1,0),与⊙C相切于点D,
过点A(—1,0),与⊙C相切于点D,
(1)求∠CAD的度数。
(2)求直线
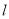 的解析式。
的解析式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.

(1)求抛物线的解析式;
 (2)求△MCB的面积S△MCB.
(2)求△MCB的面积S△MCB. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,是分解因式的为( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.x2﹣16+3x=(x+4)(x﹣4)+3x
D.10x2﹣5x=5x(2x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣3x﹣4=0的解是__.
相关试题

